Ley de Cosenos – Ejercicios Resueltos

ley de cosenos

En el artículo anterior hablamos sobre la ley de senos y hoy le toca el turno a la ley de cosenos, una de las leyes también importantes en la trigonometría y geometría, necesaria para poder comprender las reglas que implica todo triángulo oblicuángulo (obtusángulo y acutángulo), es también conocida como una generalización del teorema de pitágoras.

Para utilizar la ley de cosenos en la resolución de problemas, es necesario entender que la podemos aplicar cuando tengamos los siguientes dos casos :

Tener todos los lados y no tener un ángulo en común
Tener dos lados y el ángulo comprendido entre ellos

Fórmula para la Ley de Cosenos

La fórmula será la siguiente:

$\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos \gamma$

$\displaystyle {{a}^{2}}={{c}^{2}}+{{b}^{2}}-2bc\cos \alpha$

$\displaystyle {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cos \beta$

ley de cosenos 1

Hay que tener en cuenta que la relación que nos proporciona ésta ley, puede ser para diversas variables, no casarse con la idea de que los lados tienen que ser ABC, (a, b, c), si no que también pueden tener otras literales. Es por ello muy importante tener en cuenta lo siguiente:

Para encontrar un lado, basta con elevar al cuadrado las variables de los otros dos lados, menos el producto de ambas variables, por el coseno del ángulo que es opuesto al lado que deseamos encontrar.

Bien… Pero para entender mejor, hagamos el siguiente ejercicio

1.- En el siguiente triángulo ABC, a = 13 cm, c = 19cm, <B = 55° , Resuelva el triángulo

ley cosenos 1

Solución: Para poder resolver el siguiente ejercicio, asumimos que el lado que deseamos encontrar es el lado b, puesto que el ángulo opuesto es B, entonces nuestra fórmula queda:

$\displaystyle {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cdot \cos B$

De esto resulta

$\displaystyle {{b}^{2}}={{13}^{2}}+{{19}^{2}}-2(13)(19)\cdot \cos (55{}^\circ )$

$\displaystyle {{b}^{2}}=169+361-494(0.5735)$

Por lo que:

$\displaystyle {{b}^{2}}=246.6532$

$\displaystyle b=15.7052cm$

Ahora tenemos los tres lados de nuestro triángulo, pero nos hace falta conocer los ángulos, para ello, considero un ángulo que deseo calcular que bien puede ser el ángulo A o el ángulo C.

En este caso, elegiré el ángulo A, por lo que mi ecuación quedará:

$\displaystyle {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cdot \cos A$

Sin embargo, el valor del lado a, b y c ya los tengo, entonces procedo a despejar el coseno de A, para resolver.

$\displaystyle {{a}^{2}}-{{b}^{2}}-{{c}^{2}}=-2bc\cdot \cos A$

Despejando aún más…

$\displaystyle \frac{{{a}^{2}}-{{b}^{2}}-{{c}^{2}}}{-2bc}=\cos A$

Invirtiendo la ecuación

$\displaystyle \cos A=\frac{{{a}^{2}}-{{b}^{2}}-{{c}^{2}}}{-2bc}$

Listo, ahora es momento de sustituir nuestros valores:

$\displaystyle \cos A=\frac{{{13}^{2}}-{{15.7052}^{2}}-{{19}^{2}}}{-2(15.7052)(19)}=0.7350$

Ahora aplicando coseno inverso.

$\displaystyle A={{\cos }^{-1}}(0.7350)=42.69{}^\circ$

Por lo que el ángulo A, es de 42.69 grados.

Ahora mediante la suma de ángulos internos en un triángulo, aplicamos la propiedad para encontrar el ángulo restante:

$\displaystyle \angle A+\angle B+\angle C=180{}^\circ$

$\displaystyle 42.69{}^\circ +55{}^\circ +\angle C=180{}^\circ$

Despejando a <C

$\displaystyle \angle C=180{}^\circ -42.69{}^\circ +55{}^\circ =82.31{}^\circ$

Por lo que nuestro ejercicio está resuelto. Tenemos el triángulo completo

Aplicación de la ley de senos y cosenos

Al igual que la ley de senos, la ley de cosenos puede aplicarse para diversos problemas de la vida cotidiana, para ello colocaremos un ejemplo ilustrativo y su resolución:

2.- La distancia entre 2 puntos A y B es de 20 km. Los ángulos de elevación de un globo con respecto a dichos puntos son de 58°20′ y 67°32′. ¿A qué altura del suelo se encuentran?

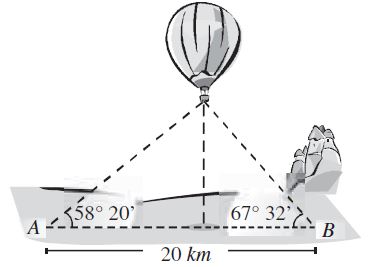
ley de cosenos 2

Solución: Podría tratarse de un problema, sumamente complicado… Pero, no lo es. Por lo tanto procedemos a aplicar la ley de senos… No sin antes, convertir nuestros grados – minutos a grados decimales.

<A = 58°20′ = 58.3333

<B =67°32′ = 67.5333

Comprobamos el ángulo faltante.

$\displaystyle \angle A+\angle B+\angle C=180{}^\circ$

$\displaystyle \angle C=180{}^\circ -\angle A-\angle B$

Sustituyendo valores

$\displaystyle \angle C=180{}^\circ -58.33{}^\circ -67.33{}^\circ =54.34{}^\circ$

Ahora, tenemos los 3 ángulos completos.

Vamos a calcular el lado a, que sería el lado opuesto al ángulo A

No podríamos aplicar la ley de cosenos, porque nos haría falta un lado forzosamente, por lo tanto recurrimos aplicar la ley de senos.

$\displaystyle \frac{a}{senA}=\frac{b}{senB}=\frac{c}{senC}$

Tenemos los 20Km que el problema nos da de referencia, y tenemos el ángulo opuesto a ese lado, que es el que encontramos de 54.34°, entonces tomamos esos datos para aplicar la ley de senos, a cualquier otro lado.

$\displaystyle \frac{a}{senA}=\frac{c}{senC}$

Despejando “a”

$\displaystyle a=\frac{c\cdot senA}{senC}$

Sustituyendo valores:

$\displaystyle a=\frac{20km\cdot sen(58.33{}^\circ )}{sen(54.34{}^\circ )}=20.95km$

Por lo que, el lado a mide 20.95 kilómetros.

Ahora podemos aplicar la función seno del ángulo 67.53 para obtener el cateto opuesto, que sería nuestra altura.

$\displaystyle sen67.53{}^\circ =\frac{h}{20.95km}$

despejando h = altura del globo

$\displaystyle h=(sen67.53)(20.95km)=19.36km$

Por lo que la altura del globo, es de 19.4 kilómetros aproximadamente (Redondeando).

Ahora es momento de practicar, resuelve los siguientes ejercicios.

Click Aquí para descargar

Fisimat,El mejor blog de física y matemáticas.

Ley de Cosenos – Ejercicios Resueltos

Fórmula para la Ley de Cosenos

Aplicación de la ley de senos y cosenos

Click Aquí para descargar

Trending Articles

Mi 530d no arranca, códigos de avería

Ley Memoria Histórica o Democrática 2022 – Matrimonios con españoles – Cuba...

Coronel de la Guardia Nacional asume dirección de Polibolívar

TELEVISOR KONKA 43 PULG TV5-43K2 - 850.00USD

Silent Hill 2: Revelation (2012) 720p BRRip Dual Español Latino-Inglés

Merluzas en Airfryer con sofrito de pimientos rojos

[Wii] Silent Hill Shattered Memories [NTSC][WBFS][ESPAÑOL][MEGA]

Gobernador de Anzoátegui decreta 14 de noviembre como feriado no laborable

The Cranberries – When You’re Gone-Pronunciación Letra Traducción

QUÉDATE, BUEN JESÚS. Autor: Luis Iruarrízaga

Matan a dos personas en colonia Reparto Lempira, San Pedro Sula

Profetas de la Ciencia Ficción (Serie) Castellano

Fallece en Mérida el empresario Alvaro Juanes Ancona

ACTIVIDAD: El primer milagro de Jesús (para los más chiquitos)

Elodia, ahora en Playboy

Reguetoneros y productores que perdieron la vida

Coche de sustitucion en BMW al pasar campaña EGR

CDG INTERROGA A ZETA SECUESTRADOR DE TAMPICO

Ayuda!!!! Notificacion de Demanda Coppel

"MI VIDA FUE SIGNADA POR LA TRISTEZA Y LA POBREZA"