Ley de Senos – Ejercicios Resueltos

ley de senos

El descubrimiento de la ley de senos dio gran paso a grandes descubrimientos de la geometría plana, y con ello la solución a muchos problemas que implicaban el cálculo de longitudes y ángulos, es por ello que el día de hoy hablaremos exclusivamente sobre la ley de senos, y de como aplicarlo a un caso especial para la primera condición de equilibrio.

Una de las cosas que debemos saber acerca de la ley de senos, es que solo es aplicable a triángulos oblicuángulos, es decir aquellos triángulos los cuales no tienen ningún ángulo recto o de 90°.

También debemos considerar dos puntos importantes, para poder utilizar dicha ley, y consiste en aplicarla solo cuando nos encontramos bajo los siguientes dos casos:

Cuando los datos conocidos son dos lados y el ángulo opuesto a uno de ellos.
Cuando se tenga dos ángulos y cualquier lado.

Fórmula para la Ley de Senos

La fórmula para resolver ejercicios de triángulos mediante la ley de senos, es la siguiente:

$\displaystyle \frac{a}{senA}=\frac{b}{senB}=\frac{c}{senC}$

ley de senos 1

Ejemplos resueltos de la Ley de Senos

1.- En el triángulo ABC, b = 15 cm, <B = 42°, y <C = 76°. Calcula la medida de los lados y ángulos restantes

Click para agrandar imagen

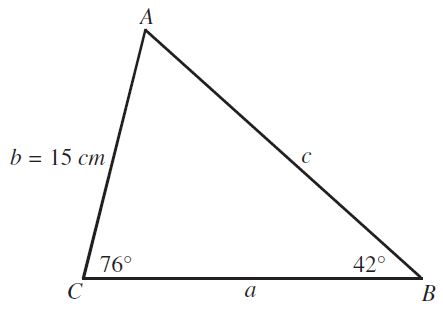
Solución: Si observamos, podemos ver que nuestro triángulo tiene dos ángulos y un solo lado, por lo cual podemos aplicar la ley de senos, sin embargo, podemos realizar un análisis sencillo para hallar el otro ángulo desconocido, tomando en cuenta que; la suma de los ángulos interiores de cualquier triángulo deben sumar 180°.

$\displaystyle \angle A+\angle B+\angle C=180{}^\circ$

Colocando, los datos que tenemos en nuestro triángulo.

$\displaystyle \angle A+42{}^\circ +76{}^\circ =180{}^\circ$

$\displaystyle \angle A+118{}^\circ =180{}^\circ$

$\displaystyle \angle A=180{}^\circ -118{}^\circ =62{}^\circ$

Por lo que el ángulo en A, es de 62 grados.

$\displaystyle \angle A=62{}^\circ$

Ahora tenemos que encontrar el valor de las longitudes de a y c, para ello recurriremos a la fórmula:

$\displaystyle \frac{a}{senA}=\frac{b}{senB}=\frac{c}{senC}$

Si observamos, nos interesa encontrar el valor del lado a y c, y ya tenemos a nuestra disposición cuanto equivalen los ángulos opuestos a esos lados, por lo cual, puedo tomar la igualdad que yo desee.

Supongamos que necesito encontrar el lado a entonces, hacemos:

$\displaystyle \frac{a}{sen62{}^\circ }=\frac{b}{sen42{}^\circ }$

Por lo que sustituyendo procedemos a despejar.

$\displaystyle a=\frac{b\cdot sen62{}^\circ }{sen42{}^\circ }=19.79cm$

Listo…! hemos encontrado el valor del lado a.

Ahora encontremos el lado restante.

$\displaystyle \frac{a}{senA}=\frac{c}{senC}$

$\displaystyle \frac{19.79cm}{sen62{}^\circ }=\frac{c}{sen76{}^\circ }$

despejando a “c”

$\displaystyle c=\frac{(19.79cm)(sen76{}^\circ )}{sen62{}^\circ }$

realizando la operación:

$\displaystyle c=\frac{(19.79cm)(sen76{}^\circ )}{sen62{}^\circ }=19.75cm$

por lo que el lado restante “c” mide 19.75 cm.

Problema resuelto.

2.- En el triángulo ABC, b = 15 cm, <B = 42°, y <C = 76°. Calcula la medida de los lados y ángulos restantes

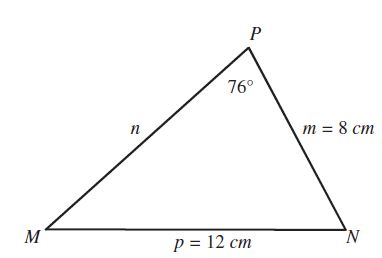
click para agrandar imagen

En este ejemplo a diferencia del anterior, no disponemos de dos ángulos, solamente de dos lados, por lo cual no podemos sumar los ángulos internos, e iniciar el proceso como se hizo anteriormente.

Pero el problema nos proporciona un lado p = 12cm, y el ángulo opuesto a éste de 76°, por lo que podemos obtener otro ángulo, mediante la fórmula de senos.

$\displaystyle \frac{p}{senP}=\frac{m}{senM}=\frac{n}{senN}$