Fisimat | Blog de Física y Matemáticas

Tiene mucho tiempo que no hemos publicado un artículo en el blog de Fisimat, así que hemos aprovechado el comienzo de año para poder redactar acerca de las nuevas que tenemos en fisimat y de las cosas grandes que estaremos creando para este año, que estamos muy decididos de dar un paso aún mayor que al anterior.

Antes que nada, queremos oficializar que nuestro sitio web se encuentra actualmente pasando en buen momento después de la mala racha que tuvimos a finales de año, al tener nuestro servidor caído y que nos causó mucha tristeza pues teníamos poco por hacer, que afortunadamente pudimos migrar a un VPS (Servidor Privado Virtual), donde ahora podemos darnos el lujo de soportar más tráfico, mejora de analítica, rendimiento y muchas cosas más que explicaremos en futuro o en el sitio web de CarlosJulians.

Este es un año de materialización de ideas y seguimos trabajando en ello.

Plataforma de Cursos en un 90% lista.

Hemos terminado nuestra plataforma en un 90%, y el proceso ha sido un poco complicado al principio pero paulatinamente hemos culminado el sitio, te invitamos a que te registres y tratar de vincular tu cuenta mediante Facebook o registro normal, y poder gozar de nuestros cursos gratuitos para que aprendes y estés al día.

Click aquí para registrarte.

Si no has podido registrarte, hemos grabado un video para ti.

Aunque es posible tomar un curso completo, estamos todavía depurando algunas partes de código de la plantilla base para poder tener más herramientas al momento de compartir videos, y ejercicios a los alumnos. Así como preguntas y un foro de discusión que en términos de funcionamiento vamos terminando poco a poco.

Este año tenemos muy en cuenta varios factores que son meta y propósito de año.

Celebrar nuestro tercer aniversario en Febrero de 2017
Subir vídeos al canal de Youtube en temas de Física y Matemáticas
Incorporar el proyecto Ingtelecto como plataforma de educación superior e ingeniería (de esto hablamos abajo).
Cursos de ingreso a la universidad 2017

Ingtelecto un proyecto para ingeniería.

Fue hace algunos meses cuando el nombre de este proyecto no estaba tan definido y pensamos en modificarlo, más de una vez, de hecho compramos un dominio con el nombre de ingenierox, pero por motivos de compra y venta del dominio con la empresa donde lo habíamos adquirido decidimos cambiar nuevamente, hasta quedar seguros con el nombre de Ingtelecto.com, una plataforma que tiene el mismo rol o giro que Fisimat, solo que para temas un poco más específicos de ingeniería.

Hace poco cambiamos algunas cosas dentro de Ingtelecto, y hemos aprovechado en modificar la estructura y en parte de código que poco a poco irá en mejora.

Aquí puedes leer algo al respecto: ¿De qué trata Ingtelecto?

Gracias por estar con nosotros

Fisimat está hecha para la comunidad estudiantil, para aquellos curiosos que no se quedan con lo que les enseñan en clases, para aquellos que buscan algo más que lo que dicta el profesor, fisimat está hecho para todos, para cualquier edad.

Gracias!!

Fisimat,El mejor blog de física y matemáticas.

Hoooola!, hoy hablaremos de un tema que se conoce como límites, pero no nos enfocaremos en su definición, ni en su explicación informal con épsilon-delta, sino que hablaremos de la parte algebraica, y trigonométrica para poder hacer artificios matemáticos (no magia), que nos ayuden a resolver problemas de indeterminación, y eso es muy importante, ya que si un límite se nos indetermina tenemos que buscar la solución.

Así que antes de comenzar, te voy a sugerir que descargues la siguiente lista de identidades trigonométricas que hemos hecho con cariño para ti

Eso no es todo, también es necesario tener en cuenta los límites notables, y saber en que momento aplicarlos, para ello colocaré los que más se usan, si conoces más, es porque muchos se deducen de los aquí propuestos.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{senx}{x}=1$
$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\cos x}{x}=0$
$\displaystyle \underset{x\to \infty }{\mathop{\lim }}\,{{\left( 1+\frac{1}{x} \right)}^{x}}=e$
$\displaystyle \underset{t\to 0}{\mathop{\lim }}\,{{\left( 1+t \right)}^{\frac{1}{t}}}=e$
$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{e}^{kx}}-1}{x}=k$
$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{a}^{kx}}-1}{x}=k\ln a$
$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\ln \left( \frac{1+x}{x} \right)=1$

Si ya has descargado el material, y tienes en cuenta los límites notables entonces es momento de ver unos ejemplos resueltos:

Ejemplo de Límites Indeterminados 0/0

Resolver

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}}{\cos x-1}$

Solución:

Como el tema que estamos viendo es sobre indeterminación de la forma 0/0, es lógico que al evaluar obtengamos la indeterminación, así que lo primero que haremos es pensar un poco en lo que tenemos y tener en cuenta que si tenemos:

$\displaystyle \cos x-1$

Lo más accesible, es recurrir a su complemento para formar una diferencia de cuadrados en el denominador pues es más fácil llegar así a un límite notable, entonces hacemos lo siguiente:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}}{\cos x-1}\cdot \frac{\cos x+1}{\cos x+1}$

Haciendo la operación, tenemos.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}}{\cos x-1}\cdot \frac{\cos x+1}{\cos x+1}=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{{{\cos }^{2}}-1}$

De la identidad pitagórica nosotros observamos que:

$\displaystyle se{{n}^{2}}x+{{\cos }^{2}}x=1$

Despejando a seno cuadrado de x.

$\displaystyle se{{n}^{2}}x=1-{{\cos }^{2}}x$

Pero esto no se parece a lo que obtuvimos en el denominador de nuestro límite, peeeeero hay una solución y eso es factorizar el signo para que el límite nos quede de la siguiente forma:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{-\left( 1-{{\cos }^{2}}x \right)}$

Ahora hacemos el cambio por seno cuadrado de x.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{-\left( 1-{{\cos }^{2}}x \right)}=\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{-se{{n}^{2}}x}=-\underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}\left( \cos x+1 \right)}{se{{n}^{2}}x}$

Por los límites notables, sabemos que:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{senx}{x}=1$

Aplicamos entonces la división de nuestro límite por $\displaystyle {{x}^{2}}$

$\displaystyle -\underset{x\to 0}{\mathop{\lim }}\,\frac{\frac{{{x}^{2}}\left( \cos x+1 \right)}{{{x}^{2}}}}{\frac{se{{n}^{2}}x}{{{x}^{2}}}}=-\underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x+1}{\frac{se{{n}^{2}}x}{{{x}^{2}}}}$

Y esto lo podemos aplicar de la siguiente forma:

$\displaystyle -\frac{\underset{x\to 0}{\mathop{\lim }}\,\left( \cos x+1 \right)}{\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}}=-\frac{2}{1}=-2$

Por lo que la respuesta de nuestro límite es -2.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{{{x}^{2}}}{\cos x-1}=-2$

Resolver

2. $\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}$

Solución:

Cómo sabemos que la inversa de el coseno es la secante, y como se trata de cero, entonces nos dará 1 de la misma forma, por lo que el límite nuevamente se indetermina, como era de esperarse, ahora para poder darle solución a este haremos lo siguiente. “Cambiar todo a Cosenos”.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1-\frac{1}{\cos x}}{{{x}^{2}}\frac{1}{\cos x}}$

y haremos la resta de fracciones del numerador:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1-\frac{1}{\cos x}}{{{x}^{2}}\frac{1}{\cos x}}=\frac{\frac{\cos x-1}{\cos x}}{\frac{{{x}^{2}}}{\cos x}}$

Aplicando la ley de la torta-herradura

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1-\frac{1}{\cos x}}{{{x}^{2}}\frac{1}{\cos x}}=\frac{\frac{\cos x-1}{\cos x}}{\frac{{{x}^{2}}}{\cos x}}=\frac{\cos x(\cos x-1)}{\cos x\cdot {{x}^{2}}}$

Simplificando

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x(\cos x-1)}{\cos x\cdot {{x}^{2}}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{{{x}^{2}}}$

Y este límite va obteniendo una forma similar al del ejemplo 1, y al multiplicarlo por su conjugado obtenemos lo siguiente:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{{{x}^{2}}}\cdot \frac{\cos x+1}{\cos x+1}=\frac{{{\cos }^{2}}x-1}{{{x}^{2}}\left( \cos x+1 \right)}$

Fácilmente hacemos el cambio por la identidad pitagórica

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}\left( \cos x+1 \right)}$

Luego hacemos…

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}\left( \cos x+1 \right)}=\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\cos x+1}$

Y evaluamos

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\cos x+1}=(1)\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{1}{\cos x+1}=1\cdot \frac{1}{2}=\frac{1}{2}$

Esto quiere decir que nuestro límite es 1/2

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{1-\sec x}{{{x}^{2}}\sec x}=\frac{1}{2}$

Resolver

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{3{{x}^{3}}{{\csc }^{2}}x}$

Solución:

Al plantearse el problema anterior, y sabiendo que podemos pasar la función cosecante a seno, tenemos entonces:

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{3{{x}^{3}}{{\csc }^{2}}x}=\frac{\cos x-1}{3{{x}^{3}}\cdot \frac{1}{se{{n}^{2}}x}}=\frac{\cos x-1}{\frac{3{{x}^{3}}}{se{{n}^{2}}x}}$

Ahora aplicamos la ley de la torta

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{\frac{3{{x}^{3}}}{se{{n}^{2}}x}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x\left( \cos x-1 \right)}{3{{x}^{3}}}$

Podemos hacer que la x que está al cubo, se haga como el producto de x al cuadrado por x, y obtenemos

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{\frac{3{{x}^{3}}}{se{{n}^{2}}x}}=\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x\left( \cos x-1 \right)}{3{{x}^{2}}\cdot x}=\frac{1}{3}\underset{x\to 0}{\mathop{\lim }}\,\frac{se{{n}^{2}}x}{{{x}^{2}}}\cdot \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{x}$

Pero de aquí podemos observar lo siguiente

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{x}=\underset{x\to 0}{\mathop{\lim }}\,\frac{-\left( 1-\cos x \right)}{x}=-\left( 0 \right)=0$

Por lo que nuestro límite converge en cero.

$\displaystyle \underset{x\to 0}{\mathop{\lim }}\,\frac{\cos x-1}{3{{x}^{3}}{{\csc }^{2}}x}=0$

Intenta resolver los siguientes límites:

Entra a los vídeos para ver la solución de cada uno:

Solución al Límite 1

Solución al Límite 2

Solución al Límite 3

Solución al Límite 4

Fisimat,El mejor blog de física y matemáticas.

Heyyy!! En el artículo nuevo de hoy hablaremos sobre el cálculo diferencial, Cuando se inicia el tema de derivadas y su interpretación geométrica, escucharás el tema sobre la “Regla de los Cuatro Pasos” que consiste en encontrar la derivada de cualquier función a partir de su definición

Al principio puede ser una tarea muy tediosa, pero es esencial para poder comprender el origen de la derivada de cualquier función, seguramente también te estarás preguntando ¿Por qué no solamente utilizar las fórmulas?, es correcto; pero sin la regla de los cuatro pasos no habría derivada alguna, pues todas proceden de ahí, es por eso que se necesita comprender al menos el concepto y de ahí realizar derivadas para poder practicar, para ello empezaremos conociendo el problema fundamental.

La derivada tiene su origen en la física y en las matemáticas, para la física de Newton era importante conocer la velocidad instantánea de cualquier objeto, pues era sumamente complicado en esos tiempos encontrar ese concepto de velocidad, y por otro lado se encontraban los matemáticos queriendo entender el concepto que los griegos ya habían tenido en el siglo III a.c, que se fundamentaba en lo mismo, y era saber el como una recta secante se podría convertir en una recta tangente moviendo solo un punto.

A partir de esas dudas se concluyó lo siguiente:

$\displaystyle \underset{h\to 0}{\mathop{\lim }}\,\frac{f(x+h)-f(x)}{h}$

No es difícil de interpretar, y de aquí surge todo, observa:

Sumamos el incremento (paso 1 ) $\displaystyle f(x+h)$
Restamos la función original (paso 2) $\displaystyle -f(x)$
Dividimos entre el incremento (paso 3) $\displaystyle h$
Evaluamos el límite cuando se tiende a cero (paso 4) $\displaystyle \underset{h\to 0}{\mathop{\lim }}\,$

En otros casos, también puedes ver la derivada usando incrementos.. Pero es lo mismo, exactamente lo mismo.

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f(x+\Delta x)-f(x)}{\Delta x}$

Pero para entenderlo mejor, veamos con algunos ejemplos.

Regla de los 4 pasos – Ejemplos Resueltos

Ejemplo 1

1.- Encontrar la derivada de $\displaystyle y=5{{x}^{2}}$

-Primer paso (incrementamos) ¡¡OJO!! es en ambos lados

$\displaystyle y+\Delta y=5{{(x+\Delta x)}^{2}}$

-Segundo paso (restamos la función original)

$\displaystyle y+\Delta y-y=5{{(x+\Delta x)}^{2}}-5{{x}^{2}}$

Podemos seguir haciendo el otro paso, pero no tendría caso si lo hacemos ya que debemos dejar clara la expresión que tenemos hasta ahora, y es momento para desarrollar el binomio al cuadrado, así que:

$\displaystyle \Delta y=5({{x}^{2}}+2x\Delta x+\Delta {{x}^{2}})-5{{x}^{2}}$

Propiedad distributiva

$\displaystyle \Delta y=5{{x}^{2}}+10x\Delta x+5\Delta {{x}^{2}}-5{{x}^{2}}$

$\displaystyle \Delta y=10x\Delta x+5\Delta {{x}^{2}}$

– Tercer paso (dividimos entre delta de X)

$\displaystyle \frac{\Delta y}{\Delta x}=\frac{10x\Delta x+5\Delta {{x}^{2}}}{\Delta x}$

$\displaystyle \frac{\Delta y}{\Delta x}=10x+5\Delta x$

-Cuarto paso (evaluamos el límite)

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\mathop{\lim }}\,\left( 10x+5\Delta x \right)$

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta y}{\Delta x}=10x$

Por lo que la derivada es 10x. ¡¡Fácil!!

Ejemplo 2

Lo hagamos ahora un poco más rápido con otro ejemplo

2.- Encontrar la siguiente derivada $\displaystyle y=\frac{3x+2}{2x-1}$

Anotamos todos los pasos, pero iremos resolviendo paso a paso:

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{3(x+\Delta x)+2}{2x+2\Delta x-1}-\frac{3x+2}{2x-1}}{\Delta x}$

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{3x+3\Delta x+2}{2x+2\Delta x-1}-\frac{3x+2}{2x-1}}{\Delta x}$

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{(2x+1)(3x+3\Delta x+2)-(3x+2)(2x+2\Delta x-1)}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}}{\Delta x}$

Seguimos reduciendo.

Pero observa lo que nos ha quedado en el numerador:

$\displaystyle \frac{(2x+1)(3x+3\Delta x+2)-(3x+2)(2x+2\Delta x-1)}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

$\displaystyle \frac{\left( 6{{x}^{2}}+6x\Delta x+4x+3x+3\Delta x+2 \right)-\left( 6{{x}^{2}}+6x\Delta x-3x-4x-4\Delta x+2 \right)}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

$\displaystyle \frac{-7\Delta x}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

Ahora si lo colocamos en nuestro límite

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{-7\Delta x}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}}{\Delta x}$

Que es lo mismo escribirlo de la siguiente manera:

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{-7\Delta x}{\Delta x\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

Simplificando

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{-7}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

Evaluando el límite

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{-7}{\left( 2x-1 \right)\left( 2x-1 \right)}=-\frac{7}{{{(2x-1)}^{2}}}$

Por lo que la derivada es:

$\displaystyle y'=-\frac{7}{{{(2x-1)}^{2}}}$

Y que pasa si probamos con una raíz….

Ejemplo 3

Encontrar la siguiente derivada $\displaystyle y=\sqrt{x+5}$

Al poner los 4 pasos juntos, tenemos:

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\sqrt{x+\Delta x+5}-\sqrt{x+5}}{\Delta x}$

Tenemos que racionalizar, para poder simplificar el cálculo.

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\sqrt{x+\Delta x+5}-\sqrt{x+5}}{\Delta x}\cdot \frac{\sqrt{x+\Delta x+5}+\sqrt{x+5}}{\sqrt{x+\Delta x+5}+\sqrt{x+5}}$

De ahí tenemos:

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{{{\left( \sqrt{x+\Delta x+5} \right)}^{2}}-{{\left( \sqrt{x+5} \right)}^{2}}}{\Delta x\left( \sqrt{x+\Delta x+5}+\sqrt{x+5} \right)}$

Luego…

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{x+\Delta x+5-x-5}{\Delta x\left( \sqrt{x+\Delta x+5}+\sqrt{x+5} \right)}$

Por lo que:

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta x}{\Delta x\left( \sqrt{x+\Delta x+5}+\sqrt{x+5} \right)}=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{1}{\sqrt{x+\Delta x+5}+\sqrt{x+5}}$

Evaluamos el límite y eso nos da:

$\displaystyle y'=\frac{1}{2\sqrt{x+5}}$

Por lo que vendría a ser la derivada de la función original…

Si se observa no es en lo absoluto complicado, ahora es momento de practicar.

Resolver los siguientes ejercicios.

1.- $\displaystyle y=3{{x}^{3}}-2{{x}^{2}}+1$

2.- $\displaystyle y=\frac{3{{x}^{2}}+1}{2x}$

3.- $\displaystyle y=\sqrt{x-3}$

4.- $\displaystyle y=\sqrt{\frac{x+6}{x+1}}$

Fisimat,El mejor blog de física y matemáticas.

Wuuuu!! Hacemos 3 años en línea, 3 años de mucho esfuerzo y dedicación ayudando a estudiantes a aprender por su cuenta, y a que obtengan la información que necesitan a través de nuestros artículos, no es una tarea fácil porque lo hacemos lo más sencillo, digerible en toda la expresión y que al final el alumno mismo recomiende dicho post por lo fácil que se le hizo entenderlo.

A pesar de que el año 2016 no fue un año del que pudiéramos estar orgullosos, ya que muchos percances y descuidos hicieron que el blog estuviera fuera de servicio, o que nuestro propósito de culminar la guía del IPN 2016 fuera algo inútil, así como los cursos de ingreso a la universidad. Esto hizo que el ánimo a los del equipo se fuera hacía abajo, pero aun así alcanzamos cifras grandes en cuanto a tráfico por los usuarios, un total de 3.5 millones de visitas en el año, lo que para nosotros es algo muy alentador y motivador.

Para este 2017 Fisimat está empezando a crecer y a SER lo que queríamos desde el inicio, así que posiblemente veas lo siguiente en la web, a partir de este mes.

Más artículos explicados paso a paso
Para post con cierta complejidad hemos creado a ingtelecto (ingtelecto.com) – No hay fecha de lanzamiento oficial, pero pronto será.
Video de ejemplos resueltos – Suscríbete (https://www.youtube.com/channel/UCfoABxGDRo2Xn1FrY0O_Whw)
Fortalecer los cursos de Ingreso a la universidad, puedes saber más a través del siguiente link http://universidad2017.fisimat.com/
Crear una comunidad exitosa de estudiantes que quieren más.

Hay muchas cosas por las que hablar para este año, y de la cuales estamos muy pero muy comprometido, por cierto; puedes echarle un vistazo a lo que te comento de lo que habrá en Fisimat, en el siguiente artículo:

http://www.fisimat.com.mx/fisimat-en-el-2017/

El año en números

Ahora la mejor manera de resumir los años en línea de fisimat, es poniéndole un vistazo a lo que ha sucedido alrededor del 2014 – 2017.

Observemos la siguiente gráfica.

En lo que corre del año, tenemos un total de 173,801 vistas y 112,928 visitantes; lo que quiere decir que nuestros números siguen siendo impactantes para nosotros, la estimación de nuestra gráfica muestra que para el año 2017 se tenga un total de 3,000,000 millones adicionales a lo que ya tenemos.

Ahora hablemos de lo que ha pasado en este tiempo.

Hemos logrado lo siguiente:

38 Artículos (posts)
3,904,870 Visitas en el 2014 – 2017
115,610 Visitas el mes pasado (enero)
1295 + Comentarios directamente en el blog
Una lista de más de 2000 suscriptores del blog
Nos visitan de todos lados (países hispanos) y parte de Europa

Los 7 posts más leídos

Vamos a colocar los artículos más leídos por nuestros visitantes, y porque también merece la pena que lo leas

El Post más compartido del año

Todas las guías del IPN – Descargar

Facebook ( 8651 likes)
Google (4441 + 1 )
Twitter (3321 tweets)

El futuro de Fisimat

El lema de Fisimat es – “Sigue Aprendiendo”

Y es en ello en lo que estamos enfocado para este año y el siguiente, que se basa en la construcción de contenido para todos.

Te compartimos una entrevista realizada a nuestro estudiante egresado de Fisimat:

Gracias

No podía terminar de escribir el artículo sin darte las gracias, y la verdad que estoy muy feliz porque sé que gracias a ti se ha podido construir esta comunidad, estamos muy felices por ello.

No olvides compartir este blog a más de una persona que pueda servirle como consulta.

Fisimat,El mejor blog de física y matemáticas.

Las derivadas surgieron por la incansable inquietud que tuvieron los griegos en el siglo III A.C, y posteriormente para los físicos al querer encontrar la velocidad instantánea en un determinado punto que los llevo a encontrarse con el mismo problema que se tenía en la antigüedad al querer mover una recta con un punto (P1) sobre una curva a otro punto (P2) (secante) y que aproximándose a cero del punto inicial se convertiría en una tangente.

Algo similar a la gráfica que se explicó en el post de Límites por regla de los 4 pasos

Afortunadamente para las derivadas algebraicas, trigonométricas, inversas, logarítmicas, y exponenciales ya existen reglas de derivación lo que simplifica para muchos el procedimiento tedioso para llegar a ellas, ahora en este artículo nos enfocaremos a las derivadas algebraicas.

Vamos a explicar que es cada una (favor de ver la imagen de abajo).

Es la derivada de una constante.
Es la derivada de una variable (cuando se deriva respecto a ella misma).
Es la derivada de una constante por una variable.
Es la derivada de una suma o resta (se pueden hacer individualmente)
Es la derivada de la variable elevada a una potencia.
Es la derivada de una función elevada a una potencia
Es la derivada de la raíz enésima
Es la derivada de una raíz cuadrada
Es la derivada de un producto (multiplicación).
Es la derivada de un cociente (división).
Es la derivada de una constante sobre una función
ES la derivada de una función sobre una constante.

Reglas de Derivación

El buen uso de las reglas de derivación consiste en dominar el álgebra, así que una de las cosas que le sugerimos al lector, es repasar los tópicos de potencia, radicales, factorización, productos notables y operaciones con fracciones algebraicas, para hacer el procedimiento más efectivo y conciso.

Supongamos que tenemos el siguiente ejemplo.

Ejemplos Resueltos de Derivadas Algebraicas

1.- Resuelva la siguiente derivada:

$\displaystyle y={{x}^{4}}-3{{x}^{2}}+2{{x}^{-3}}+2$

Solución:

Como se trata de una derivada con muchos términos de suma y resta, es posible hacer la derivada individual de cada término para que al final se junte y se entregue la respuesta completa de la derivada.

Para el primer término tenemos $\displaystyle {{x}^{4}}$ , podemos aplicar el caso 5 de nuestra tabla de reglas, quedando así:

$\displaystyle y'=4{{x}^{4-1}}=4{{x}^{3}}$

Después tenemos $\displaystyle 3{{x}^{2}}$

Aplicando la propiedad de la regla 3 combinada con la 5, tenemos.

$\displaystyle y'=3(2{{x}^{2-1}})=3(2x)=6x$

Por ahora nos queda realizar la siguiente derivada $\displaystyle 2{{x}^{-3}}$

Que al derivar obtenemos:

$\displaystyle -3(2{{x}^{-4}})=-6{{x}^{-4}}=\frac{-6}{{{x}^{4}}}$

Finalmente nos queda el valor de 2, que al derivar tendríamos un cero, puesto que se trata de una constante.

Ahora ordenando los términos derivados.

$\displaystyle y'=4{{x}^{3}}-6x-\frac{6}{{{x}^{4}}}$

Lo que vendría a ser nuestra derivada.

2.- Resuelva la siguiente derivada:

$\displaystyle y=\frac{3x-4}{2{{x}^{2}}+5}$

Solución:

Tenemos la derivada de un cociente, por lo tanto recordemos que para un cociente tenemos que aplicar la siguiente fórmula:

$\displaystyle \frac{u}{v}=\frac{vu'-uv'}{{{v}^{2}}}$

Al seguir los pasos tenemos:

$\displaystyle y'=\frac{(2{{x}^{2}}+5)\cdot \frac{d}{dx}(3x-4)-(3x-4)\frac{d}{dx}(2{{x}^{2}}+5)}{{{(2{{x}^{2}}+5)}^{2}}}$

Ahora proseguimos a derivar donde está indicada la operación:

$\displaystyle y'=\frac{(2{{x}^{2}}+5)\cdot (3)-(3x-4)(4x)}{{{(2{{x}^{2}}+5)}^{2}}}$

Seguimos simplificando

$\displaystyle y'=\frac{6{{x}^{2}}+15-12{{x}^{2}}+16}{{{(2{{x}^{2}}+5)}^{2}}}$

$\displaystyle y'=\frac{-6{{x}^{2}}+31}{{{(2{{x}^{2}}+5)}^{2}}}$

Con eso tendríamos nuestra derivada resuelta.

3.- Resuelva la siguiente derivada:

$\displaystyle y=(4{{x}^{4}}-3x)(-2x+1)$

Solución

Como en el caso anterior, tenemos la derivada de un producto, y ésta se resuelve aplicando lo siguiente:

$\displaystyle uv=uv'+vu\acute{\ }$

Por lo que al resolver el ejercicio anterior tenemos:

$\displaystyle y'=(4{{x}^{4}}-3x)\cdot \frac{d}{dx}(-2x+1)+(-2x+1)\cdot \frac{d}{dx}(4{{x}^{4}}-3x)$

Aplicando la derivada donde está aplicada, tenemos lo siguiente:

$\displaystyle y'=(4{{x}^{4}}-3x)(-2)+(-2x+1)(16{{x}^{3}}-3)$

Posteriormente tendríamos:

$\displaystyle y'=(-8{{x}^{4}}+6x)+(-32{{x}^{4}}+16{{x}^{3}}+6x-3)$

Que simplificando este se convierte en:

$\displaystyle y'=-8{{x}^{4}}+6x-32{{x}^{4}}+16{{x}^{3}}+6x-3$

Y finalmente tendríamos lo siguiente:

$\displaystyle y'=-40{{x}^{4}}+16{{x}^{3}}+12x-3$

4.- Resuelva la siguiente derivada:

$\displaystyle y={{(-\frac{3}{4}{{x}^{2}}+2x-1)}^{3}}$

Solución:

En este caso tenemos la derivada de una potencia, y por fórmula sabemos que se aplica lo siguiente:

$\displaystyle {{u}^{n}}=n{{u}^{n-1}}u'$

Siguiendo la fórmula, podemos aplicarla para nuestra derivada y esto quedaría de la siguiente manera:

$\displaystyle y'=3{{(-\frac{3}{4}{{x}^{2}}+2x-1)}^{2}}\cdot \frac{d}{dx}(-\frac{3}{4}{{x}^{2}}+2x-1)$

Proseguimos a derivar lo que queda en el término final

$\displaystyle y'=3{{(-\frac{3}{4}{{x}^{2}}+2x-1)}^{2}}(-\frac{6}{4}x+2)$

Finalmente esto lo podemos dejar expresado como un producto, de la siguiente manera:

$\displaystyle y'=(-\frac{18}{4}+6){{(-\frac{3}{4}{{x}^{2}}+2x-1)}^{2}}$

Por lo que esto finalmente sería la derivada de la función.

— Ahora es momento de que veas unos videos y entiendas mejor aún del tema:

Aprender derivadas no es en lo absoluto complicado, simplemente debemos las reglas de derivación que se presenten, es lo único que puede dificultar resolver una derivada, pero después de eso es extraño tener derivadas complicadas, más adelante en otro artículo veremos otro tipo de derivadas que tienen un nivel de complejidad un poco más alto de lo normal.

Fisimat,El mejor blog de física y matemáticas.

Hace algunos meses publicábamos sobre las integrales por sustitución, las cuales puedes leer aquí mismo , en este ocasión vamos a tocar un tema relacionado con integrales pero aplicando el método “Por Partes”, ya que es uno de los métodos que tienen mucha aplicación en diversas áreas de ingeniería, el método por partes SIEMPRE se aplica para un producto entre dos funciones, es ahí donde radica la fórmula e integración por éste método.

Veamos como se obtiene:

Sea

$\displaystyle y=uv$

Dónde

$\displaystyle u=f(x)$

$\displaystyle v=g(x)$

Sabemos entonces que por la derivada de un producto.

$\displaystyle \frac{d}{dx}\left[ f(x)g(x) \right]=f(x)g'(x)+g(x)f'(x)$

Y de esta misma tenemos que integrarla, quedando así:

$\displaystyle \int{\frac{d}{dx}\left[ f(x)g(x) \right]dx}=\int{f(x)g'(x)dx}+\int{g(x)f'(x)dx}$

$\displaystyle f(x)g(x)=\int{f(x)g'(x)dx}+\int{g(x)f'(x)dx}$

Despejamos a:

$\displaystyle \int{f(x)g'(x)dx}$

Para mayor comodidad, quedando así:

$\displaystyle \int{f(x)g'(x)dx}=f(x)g(x)-\int{g(x)f\acute{\ }(x)dx}$

Escribiéndolo en término de diferenciales, sabemos que:

$\displaystyle du=f'(x)dx$

$\displaystyle dv=g'(x)dx$

Quedando asi:

$\displaystyle \int{udv}=uv-\int{vdu}$

Ahora, antes de comenzar a resolver ejercicios donde apliquemos el método de por partes, es necesario tener en cuenta lo siguiente: Es muy probable que de la integral original nos quede una integral más, es decir; no en el primer intento de integración obtenemos el resultado, nos puede quedar otra integral más y seguiremos resolviendo.

Ahora, a pesar de que no existe una regla correcta para poder comprobar la variable adecuada en nuestra elección para U, o dV, hay algunos criterios funcionales que aplica en la mayor parte para las integrales por partes, estos criterios son.

1.- Para integrales que tienen la forma:

$\displaystyle \int{p(x)\ln xdx}$

$\displaystyle \int{p(x)arcsenxdx}$

$\displaystyle \int{p(x)arccosxdx}$

$\displaystyle \int{p(x)arctanxdx}$

Donde p(x) es un polinomio, se recomienda siempre hacer U a la función trascendente, mientras que dv = p(x) [El polinomio]

2.- Para integrales que tienen la forma:

$\displaystyle \int{p(x){{e}^{ax}}dx}$

$\displaystyle \int{p(x)senxdx}$

$\displaystyle \int{p(x)\cos xdx}$

En donde p(x) es un polinomio, se recomienda siempre hacer u = p(x), mientras que dv a la función trigonométrica o exponencial.

3.- Apoyarse del acrónimo LIATE

Dónde:

L = Logarítmicas

I = Inversas

A = Algebraicas

T = Trigonométricas

E = Exponenciales

Con este criterio podemos establecer para nosotros quien debe ser U, de izquierda a derecha, es decir primero buscamos que haya logarítimicas, sino pasamos al segundo que es inversas, luego algebraicas y así sucesivamente.

Ejercicios Resueltos de Integrales Por Partes

En el siguiente ejemplo se resuelven las dos siguientes integrales:

1.- $\displaystyle \int{x{{e}^{x}}dx}$

2.- $\displaystyle \int{{{x}^{3}}\ln x}dx$

Solución:

También se resuelve las siguientes integrales:

$\displaystyle \int{{{x}^{2}}{{e}^{x}}dx}$

$\displaystyle \int{{{x}^{2}}\cos xdx}$

$\displaystyle \int{{{e}^{x}}senxdx}$

$\displaystyle \int{{{e}^{2x}}sen3xdx}$

$\displaystyle \int{x\arctan dx}$

Fisimat,El mejor blog de física y matemáticas.

En Fisimat nos preocupamos por la creación de contenido de calidad y que de alguna u otra forma aporte al estudiante, es por eso que hemos realizado con mucho esfuerzo la creación de 150 vídeos de cálculo diferencial e integral, que están variados en cuanto a los temas de tal forma que el estudiante adquiera la habilidad necesaria y refuerce sus conocimientos, es muy recomendable que el alumno tenga al menos conocimiento mínimo de algunos temas.

Pues muchos vídeos tienen alguna complejidad, pero nada del otro mundo que un alumno hábil pueda resolver, es por ello que estaremos organizando los vídeos de tal forma que no haya problema alguno al momento de que una persona quiera ver los vídeos de comienzo a final. Los temas de cálculo están organizados por dos ramas, una está dedicada al #MaratonDeIntegrales y la otra al #MaratonDeDerivadas de tal forma que logremos juntar la mayor cantidad de vídeos con estos temas para todos.

Quizá realizar una biblioteca de vídeos, la más grande que pueda haber en la red de youtube, y es un trabajo muy pesado pero importante para el Team De Fisimat.

Puedes ver los vídeos directamente de la lista de Reproducción en Youtube.

El formulario que se ocupa en el curso, es el siguiente: Click para descargar Formulario de Cálculo

En Fisimat tenemos planes para este año y son los siguientes:

Grabar +100 videos de Cálculo Vectorial
Grabar +150 videos de Ecuaciones Diferenciales
Grabar +100 vídeos de Pre-Cálculo

Esperamos poder grabar este serie de vídeos en los siguientes meses. Aquí mostrados en nuestra pequeña Agenda.

Cálculo Vectorial – Meses de (Mayo-Agosto) – 2017
Ecuaciones Diferenciales – Meses de (Septiembre – Diciembre) – 2017

Iremos también alternando un poco los vídeos para que podamos subir material exclusivo en el área de Álgebra Lineal (reforzar los temas que están expuestos ahí) y también agregar un poco de contenido a la sección de Pre-Cálculo.

Dentro de nuestros artículos hay también explicación paso a paso a los temas abordados en Cálculo.

Aquí puedes ver el siguiente Post:

Integrales por Cambio de Variable o Sustitución

Integrales por Partes

Cualquier cosa relacionada al artículo, se harán las modificaciones pertinentes.

“Sigue Aprendiendo”.

Fisimat,El mejor blog de física y matemáticas.

Bien, después de no publicar en cierto tiempo. Hemos decidido publicar el tema de fracciones parciales ya que es de vital importancia para poder comprender uno de los temas de integración por éste método.

Sabemos que es uno de los temas muy importantes en las matemáticas de nivel media superior o de introducción a la universidad también les llaman “preuniversidad”. Es sin duda el tema de las fracciones parciales que serán ocupadas más adelante en temas de integración y transformadas de Laplace. (lo último se mira en la universidad en áreas de ingeniería o ciencias puras).

La descomposición de fracciones parciales es una técnica algebraica que puede utilizarse para descomponer un producto de expresiones racionales en una suma de expresiones racional más simples.

Una expresión racional es aquella en la que tanto el numerador como su denominador son polinomios. Y ahora una expresión racional apropiada es aquella en la que el grado del numerador es estrictamente menor que el grado del denominador.

Ahora veamos como podemos aprender las fracciones parciales, y dividiremos nuestro post en 5 partes. Ya que existen varias clasificaciones respecto a los grados del denominador

1.- Factores Lineales Distintos
2.- Factores lineales repetidos
3.- Distintos factores cuadráticos irreducibles
4.- Factores cuadráticos irreducibles repetidos
5.- Factores mixtos

Empezaremos primero con los Factores Lineales Distintos.

Factor Lineal No Repetido

Antes de comenzar hablar sobre el caso de factor lineal no repetido, es importante que sepamos de qué trata el tema en si. Para ello vamos a realizar la siguiente suma de fracciones.

$\displaystyle \frac{2}{x}+\frac{3}{x+1}$

Recordemos que para sumar esa fracción algebraica se hace mediante el producto cruzado y se suma, lo del denominador es el producto de ambos. Ejemplo!

$\displaystyle \frac{2}{x}+\frac{3}{x+1}=\frac{2(x+1)+3(x)}{x(x+1)}$

Entonces decimos que

$\displaystyle \frac{2}{x}+\frac{3}{x+1}=\frac{2(x+1)+3(x)}{x(x+1)}=\frac{2x+2+3x}{{{x}^{2}}+x}=\frac{5x+2}{{{x}^{2}}+x}$

Entonces podemos decir que

$\displaystyle \frac{2}{x}+\frac{3}{x+1}=\frac{5x+2}{{{x}^{2}}+x}$

Bien, espero que hasta este punto no haya habido algún problema al respecto de como se realizaron los pasos para obtener la suma, entonces pensemos, cómo podemos regresar la operación que hicimos y obtener el comienzo , es decir obtener las dos fracciones del comienzo

Para el caso 1 que estaremos explicando en el post, A cada factor lineal de la forma mx + n que aparezca en el denominador le corresponde una suma de fracciones de la forma A/(mx+n), donde A es una constante a determinar.

Ejercicios Resueltos de Fracciones Parciales – Caso I

Ejemplo 1: Descomponer en fracciones parciales: $\displaystyle \frac{5x+2}{{{x}^{2}}+x}$

Solución: Como ya mencionamos es encontrar la suma de fracciones que den por resultado la fracción anterior. Lo primero que demos hacer es factorizar el denominador.

$\displaystyle \frac{5x+2}{x(x+1)}$

Bien, una vez que factorizamos, tenemos abajo dos factores lineales y son lineales “Por qué no están al cuadrado” y no son repetidos, entonces corresponde al caso 1. Ahora tenemos que agregarles constantes y determinar sus valores.

Ejemplo:

$\displaystyle \frac{5x+2}{x(x+1)}=\frac{A}{x}+\frac{B}{x+1}$

Ahora procedemos a multiplicar a ambos miembros por el denominador del miembro izquierdo, y obtenemos:

$\displaystyle \frac{5x+2}{x(x+1)}\cdot x(x+1)=\frac{A}{x}\cdot x(x+1)+\frac{B}{x+1}\cdot x(x+1)$

Con esto cancelando términos similares en numerador y denominador, tenemos.

$\displaystyle 5x+2=A(x+1)+Bx$

Realizamos la operación del miembro derecho y obtenemos:

$\displaystyle 5x+2=Ax+A+Bx$

Factorizando el miembro derecho:

$\displaystyle 5x+2=x(A+B)+A$

Ahora igualamos los que tengan “x” con el miembro izquierdo y los del lado derecho, y hacemos lo mismo también para los que no tengan coeficientes.

$\displaystyle 5x=x(A+B)$

$\displaystyle 2=A$

Las “x” con las “x” las cancelamos e igualamos.

$\displaystyle 5=A+B$

Ahora podemos decir, de la segunda ecuación que A = 2, entonces podemos despejar para encontrar “B”.

$\displaystyle 5=2+B$

Por lo que el valor de B es 3

$\displaystyle B=3$

Podemos entonces decir que las dos fracciones principales, son:

$\displaystyle \frac{A}{x}+\frac{B}{x+1}=\frac{2}{x}+\frac{3}{x+1}$

Y listoooo!! Con esto ya tenemos realizados un ejercicio básico del caso 1.

Fisimat,El mejor blog de física y matemáticas.

Hablar sobre el lenguaje algebraico es hablar sobre la forma de interpretar símbolos o números de algunas expresiones matemáticas. Sin duda el lenguaje algebraico es una forma de estructurar las diversas operaciones que puedan desarrollarse con la aritmética (la suma, la resta, la multiplicación, divisón), en nuestras vidas es posible enfrentarnos a problemas de ésta índole. Por eso es vital el comprenderlo en el área del Álgebra.

De hecho es un requisito muy importante para acreditar el examen de ingreso a la universidad.

Pero como siempre en Fisimat hemos dicho, que lo mejor para entender un problema de cualquier área de matemáticas, física o química es aprendiendo a resolver ejercicios o ejemplos resueltos. Así!! que aquí vamos.

Ejemplo Resuelto del lenguaje algebraico

Supongamos que tenemos el siguiente ejemplo.

Ejemplo 1: Exprese en lenguaje algebraico lo siguiente: un número disminuido en 9

Solución: Al ser un número cualquiera, podemos representarlo con cualquier literal, puede ser una “x” o una “y”, o quizá una “z”, no importa que literal uses, porque finalmente representa a cualquier número, y a su vez ese número está disminuido o sea restado en 9. Podríamos decir entonces que eso es:

$\displaystyle x-9$

Así de fácil, si te das cuenta no hay problema alguno para no comprender las indicaciones del lenguaje algebraico, bien ahora pasemos a un ejemplo más complicado. ¡Le subamos nivel!

Ejemplo 2: Exprese en lenguaje algebraico lo siguiente: tres números consecutivos

Solución: Ya sabemos que un número cualquiera lo podemos expresar con la literal que más nos agrade, entonces seguiremos tomando a “X” como a esa literal.

Pero si observamos ahora nos dice que son tres números consecutivos. Pues bien; pongamos un ejemplo aún más claro para comprender el ejemplo, si tengo a un número digamos 3, entonces su consecutivo sería 4, y el siguiente sería 5 y luego 6, etc… Entonces viendo el problema del lenguaje algebraico diríamos

$\displaystyle x+1,x+2,x+3$

Ejemplo 3: Exprese en lenguaje algebraico lo siguiente: La raíz cúbica de la diferencia de dos números cualesquiera

Solución: Con este ejemplo nos daremos cuenta si hemos aprendido un poco por ahora, si nos piden la raíz cúbica de la diferencia de dos números cualesquiera sabemos que esos números cualesquiera serán dos incógnitas es decir que puedo tomar a “x” y también “y” , pero si es una diferencia entonces decimos que:

$\displaystyle x-y$

Hasta ahí tenemos la diferencia de dos números cualesquiera

Pero también piden su raíz cúbica

$\displaystyle \sqrt[3]{x-y}$

Perfecto, entonces tenemos ya el ejemplo resuelto.

Tenemos ahora las siguientes expresiones algebraicas que se traducirán al lenguaje común.

El triple del cuadrado de un número menos el cuádruple de otro.
La raíz cúbica de la diferencia de dos números.
El cuadrado de un número menos el cuadrado de la suma de otros dos números
El doble del cubo de la diferencia de dos números
El triple producto del cuadrado de un número por otro.
El producto de la suma de dos números por la diferencia de los mismos números.
El semiproducto de la suma de dos números por su diferencia.
El cubo de la mitad de un número
La mitad del cubo de un número
Un tercio del cuadrado de la suma de dos números.
Un tercio de la suma de los cuadrados de dos números
El cubo de la diferencia de las raíces cuadradas de dos números.

Bien las soluciones son las siguientes:

$\displaystyle \begin{array}{l}3{{x}^{2}}-4y\\\sqrt[3]{a-b}\\{{x}^{2}}-{{(a+b)}^{2}}\\2{{(x-y)}^{3}}\end{array}$

$\displaystyle \begin{array}{l}3{{a}^{2}}b\\(x+y)(x-y)\\\frac{(x+y)(x-y)}{2}\\{{\left( \frac{a}{2} \right)}^{3}}\end{array}$

$\displaystyle \begin{array}{l}\frac{{{a}^{3}}}{2}\\\frac{{{(x+y)}^{2}}}{3}\\\frac{{{x}^{2}}+{{y}^{2}}}{3}\\{{\left( \sqrt{a}-\sqrt{b} \right)}^{3}}\end{array}$

Ahora veamos la explicación más detallada en formato vídeo

Explicación en Vídeo del Lenguaje Algebraico

Pero en Fisimat no descansamos y hemos decidido sacar un vídeo de nuestro curso de ingreso a la universidad, para que aprendas de una vez por todas este tema, así que te dejamos con el siguiente video.

Por favor presta mucha atención y toma nota. Si tienes dudas no dudes en dejarla en los comentarios del Blog.

Lista de Ejercicios para Practicar

Bien, ahora es momento de poner en práctica tus conocimientos acerca del tema, es por ello que te proporcionamos la siguiente lista que podrás descargarla gratuitamente a cambio de una pequeña acción social.

Fisimat,El mejor blog de física y matemáticas.

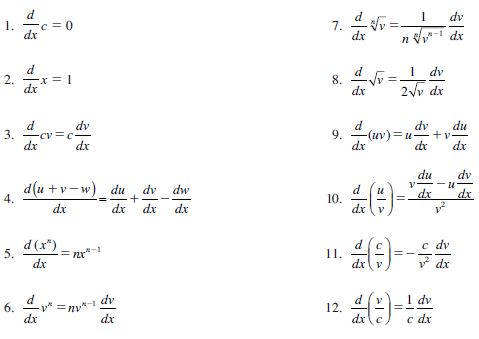
Hoy traemos un nuevo artículo relacionado a los binomios, siiii a esos que te dan dolor de cabeza cuando los escuchas, y mucho más cuando te dicen que están elevados al cuadrado o al cubo, pero bueno, en esta ocasión vas aprender a resolver binomios cuando están elevados a potencias mucho más grandes, por ejemplo a la 5, a la 8 , a la 9, etc… Y todo parte desde el gran Newton, un joven de padres granjeros el cual se le acuñe muchas cosas en cuanto a investigación e inventos, desde telescopios, leyes de la física, el desarrollo del cálculo infinitesimal, etc..

El Binomio de Newton o Ley del Binomio es un método algebraico para poder encontrar de forma rápida el resultado del producto de un mismo binomio.

Aquí nos daremos cuenta que los productos notables juegan un papel muy importante, ya que sabemos que un producto notable nos devuelve siempre el resultado de la operación entre binomios sin tener que hacer los cálculos uno por uno.

Por ejemplo citaremos el siguiente ejemplo y que quede más claro. Si tenemos el siguiente producto:

$\displaystyle (4x{{y}^{2}}+2a)(4x{{y}^{2}}-2a)$

Se trata a simple vista del producto de un binomio conjugado ¿por qué conjugado?, porque los binomios son similares a excepción de un signo (+) y un signo (-) entre los términos. Ahora que sabemos esto, podemos realizar la operación de término por término o sea aplicar la “ley distributiva”.

$\displaystyle (4x{{y}^{2}}+2a)(4x{{y}^{2}}-2a)=16{{x}^{2}}{{y}^{4}}+8ax{{y}^{2}}-8ax{{y}^{2}}-4{{a}^{2}}$

Si esto se simplifica obtendremos lo siguiente:

$\displaystyle (4x{{y}^{2}}+2a)(4x{{y}^{2}}-2a)=16{{x}^{2}}{{y}^{4}}-4{{a}^{2}}$

Si tenemos un poco de dominio del álgebra sabremos que el resultado era obvio, ¿por qué? pues sabemos que la regla de los binomios conjugados establece que el resultado es “el cuadrado del primer término menos el cuadrado del segundo”. Lo que lógicamente nos dio el resultado del binomio, sin necesidad de haber aplicado la propiedad distributiva

¿Se entendió?, bien ahora imaginemos que necesitamos obtener el resultado sin efectuar nuevamente las operaciones una por una, pero de un binomio (x+y) a cierta potencia n, en donde n debe ser un número natural o sea un número positivo. Pues aquí es donde entra el apreciado método del Binomio de Newton.

Explicación del Binomio de Newton

Ahora desarrollemos los binomios (x+y) hasta la sexta potencia, y veamos el comportamiento que tiene el binomio, de ahí nos daremos cuenta de otros puntos importantes.

$\displaystyle {{(x+y)}^{0}}=1$

$\displaystyle {{(x+y)}^{1}}=x+y$

$\displaystyle {{(x+y)}^{2}}={{x}^{2}}+2xy+{{y}^{2}}$

$\displaystyle {{(x+y)}^{3}}={{x}^{3}}+3{{x}^{2}}y+3x{{y}^{2}}+{{y}^{3}}$

$\displaystyle {{(x+y)}^{4}}={{x}^{4}}+4{{x}^{3}}y+6{{x}^{2}}{{y}^{2}}+4x{{y}^{3}}+{{y}^{4}}$

$\displaystyle {{(x+y)}^{5}}={{x}^{5}}+5{{x}^{4}}y+10{{x}^{3}}{{y}^{2}}+10{{x}^{2}}{{y}^{3}}+5x{{y}^{4}}+{{y}^{5}}$

$\displaystyle {{(x+y)}^{6}}={{x}^{6}}+6{{x}^{5}}y+15{{x}^{4}}{{y}^{2}}+20{{x}^{3}}{{y}^{3}}+15{{x}^{2}}{{y}^{4}}+6x{{y}^{5}}+{{y}^{5}}$

Hasta este punto podemos observar que

El primer término es siempre $\displaystyle {{x}^{n}}$
El segundo término tiene un comportamiento de $\displaystyle n{{x}^{n-1}}y$
Y de ahí empiezan a aparecerse algunos coeficientes y empieza a decaer el exponente del primer término y el otro empieza a aumentar.

Hasta este punto es muy importante comprender ello, porque el siguiente análisis será aún mucho mejor.

El triángulo de Pascal

Veamos el siguiente vídeo hecho por Fisimat, donde explicamos el triángulo de Pascal en honor al gran matemático francés Blaise Pascal al cual se le adjudica dicho procedimiento, bien entonces veamos algunos ejemplos resueltos de el Binomio de Newton.

Al ver este video, posiblemente ya entiendas como resolver el binomio de Newton haciendo uso del triángulo de Pascal, es por eso que vamos a desarrollar dos ejemplos más, pero ya más intuitivo, que el alumno interprete como se han resuelto para ver si el aprendizaje ha sido correcto.

Ejercicios Resueltos del Binomio de Newton

Hay un pequeño secreto también sobre las potencias del 11, pues resulta que las potencias del 11 nos darán siempre los coeficientes del triángulo de Pascal, veamos de esta manera.

Pero hay un problema cuando llegamos a la 5ta potencia, ahí los coeficientes ya no son los mismos, ahí se tiene que superponer los dígitos para poder encontrar los demás.

Ok, entonces vamos a poner a prueba nuestros conocimientos. Veamos si hemos entendido todo al 100%

1.- Desarrolle el siguiente binomio

$\displaystyle {{(2{{b}^{2}}-3a)}^{4}}$

Solución:

$\displaystyle {{(2{{b}^{2}}-3a)}^{4}}={{(2{{b}^{2}})}^{4}}+4{{(2{{b}^{2}})}^{3}}(-3a)+6{{(2{{b}^{2}})}^{2}}{{(-3a)}^{2}}+4(2{{b}^{2}}){{(-3a)}^{3}}+{{(-3a)}^{4}}$

Hasta este punto hemos desarrollado a la perfección el triángulo de Pascal

Ahora empecemos a multiplicar los exponentes, por regla.

$\displaystyle {{(2{{b}^{2}}-3a)}^{4}}=16{{b}^{8}}+4(8{{b}^{6}})(-3a)+6(4{{b}^{2}})(9{{a}^{2}})+4(2{{b}^{2}})(-27{{a}^{3}})+(81{{a}^{4}})$

Evaluamos las operaciones de exponentes

$\displaystyle {{(2{{b}^{2}}-3a)}^{4}}=16{{b}^{8}}-96a{{b}^{6}}+216{{a}^{2}}{{b}^{4}}-216{{a}^{3}}{{b}^{2}}+81{{a}^{4}}$

Listo!!! Problema resuelto ¿te salió igual?, si tienes dudas dejarlo en la caja de comentarios aquí abajo.

Fisimat,El mejor blog de física y matemáticas.

Antes de adentrarnos a la ley de los exponentes es importante primero saber que los exponentes también llamado potencias, nos indicará la cantidad de veces que se multiplicará por si mismo un número o base, por citar un ejemplo sencillo.

$\displaystyle {{5}^{4}}=5\cdot 5\cdot 5\cdot 5$

Podríamos decir que 5^4 podría llamarse “5 elevado a la cuarta potencia”, “5 a la 4” o simplemente “5 a la cuarta”.

Por lo que un exponente nos salva de estar escribiendo muchas multiplicaciones de un mismo número.

$\displaystyle {{b}^{6}}=b\cdot b\cdot b\cdot b\cdot b\cdot b$

Pero para hacerlo aún más interesante, tenemos que ver las leyes que ronda a través de los exponentes. Aunque no sin antes de verificar tres puntos importantes en la exponenciación, estos tres puntos son requisito fundamental del aprendizaje de este tema, podríamos decir incluso que lo que necesitas memorizar o aprender son básicamente los puntos de abajo, después de ello lo demás sale fácil!!

pero para hacerlo mejor aún, veamos el siguiente vídeo que explica el equipo de Fisimat.

3 Datos importantes para entender los exponentes

El exponente dice cuantas veces un número se multiplicará
Un exponente negativo significa dividir, lo contrario de multiplicar aquí se tendrá que dividir,
Un exponente fraccional como 1/n significa tomar la raiz n-ésima .

Ya analizamos el punto 1, y en ese punto nos dimos cuenta realmente que una potencia dice las veces que una base se multiplica

Ahora veamos el punto 2

$\displaystyle {{x}^{-n}}=\frac{1}{{{x}^{n}}}$

Ojo esto es siempre válido, siempre y cuando x no sea cero, si x es cero, el resultado no está definido.

Ahora veamos el punto 3

$\displaystyle {{x}^{\frac{1}{n}}}=\sqrt[n]{x}$

Aquí es importante observar bien que ocurre con la potencia.

Si entendemos esos 3 puntos, entonces entenderemos a los exponentes y las leyes que se basan en esas ideas. Para no hacerlo muy teórico, hemos realizado una tabla donde podrás observar las leyes y ejemplos a su lado.

Ahora podríamos resolver el siguiente ejemplo:

Ejemplos Resueltos de Las Leyes de Exponentes

Si tenemos dudas nuevamente con el uso de las potencias, podemos ver el siguiente video para reafirmar nuestros conocimientos.

Ahora hagamos otro ejemplo más complicado.

Ejemplo 1: Simplificar la siguiente fracción algebraica

$\displaystyle \frac{{{(3{{x}^{4}}{{y}^{-2}})}^{-3}}}{{{(2{{x}^{3}}{{y}^{2}})}^{-2}}}$

Para poder simplificar debemos analizar lo siguiente, solamente tenemos potencias negativas que salen de la agrupación paréntesis, entonces lo que haremos será aplicar la ley para exponentes negativos, y con eso nos daremos cuenta que la expresión que está en el numerador pasará al denominador pero con exponente positivo, y la que está en el denominador pasará al numerador pero con exponentes positivo.

$\displaystyle \frac{{{(3{{x}^{4}}{{y}^{-2}})}^{-3}}}{{{(2{{x}^{3}}{{y}^{2}})}^{-2}}}=\frac{{{(2{{x}^{3}}{{y}^{2}})}^{2}}}{{{(3{{x}^{4}}{{y}^{-2}})}^{3}}}$

De esa forma, ya podemos aplicar las potencias a las agrupaciones.

$\displaystyle \frac{{{(2{{x}^{3}}{{y}^{2}})}^{2}}}{{{(3{{x}^{4}}{{y}^{-2}})}^{3}}}=\frac{4{{x}^{6}}{{y}^{4}}}{27{{x}^{12}}{{y}^{-6}}}$

Podemos separar los productos y aplicar las leyes básicas, para la división de potencias.

$\displaystyle \frac{4{{x}^{6}}{{y}^{4}}}{27{{x}^{12}}{{y}^{-6}}}=\frac{4}{27}\cdot \frac{{{x}^{6}}}{{{x}^{12}}}\cdot \frac{{{y}^{4}}}{{{y}^{-6}}}$

Aquí nos quedaría lo siguiente:

$\displaystyle \frac{4{{x}^{6}}{{y}^{4}}}{27{{x}^{12}}{{y}^{-6}}}=\frac{4}{27}\cdot \frac{{{x}^{6}}}{{{x}^{12}}}\cdot \frac{{{y}^{4}}}{{{y}^{-6}}}=\frac{4}{27}\cdot {{x}^{6-12}}\cdot {{y}^{4-(-6)}}$

Ahora tendríamos lo siguiente:

$\displaystyle \frac{4{{x}^{6}}{{y}^{4}}}{27{{x}^{12}}{{y}^{-6}}}=\frac{4{{x}^{-6}}{{y}^{10}}}{27}=\frac{4{{y}^{10}}}{27{{x}^{6}}}$

y listooo!!

Fisimat,El mejor blog de física y matemáticas.

El tema de las raíces es un tema sin duda que muchas veces tenemos que batallar para comprenderlo, y no solo porque sea difícil,porque no lo es, sino que muchas veces los profesores que nos enseñan este método, lo hacen complicado. Así que mediante este artículo, lo vamos a comprender de una vez por todas.

Antes de empezar vamos a detallar que un radical es la raiz indicada de una cantidad, y de aquí se desprenden dos tipos, las raíces con cantidad racional y las de cantidad irracional, las de cantidad racional son aquellas a las que le podemos sacar raiz sin ningún problema y de una forma muy rápida, y las irracionales son los radicales que difícilmente podemos sacarle raíz, normalmente terminamos expresándolas

Entonces podemos decir que la radicación es la operación inversa de la potenciación, ese tema que ya vimos en el artículo anterior donde explicábamos sobre la ley de los exponentes ,

Propiedades de los Radicales

Para poder ver las propiedades de los radicales es importante que analicemos la siguiente imagen, donde no solamente tenemos el caso de “radicación” sino que también ponemos en contraste a la potenciación, y darnos cuenta de las similitudes entre ambas, así que a tomar NOTA!!

Con esto podemos darnos cuenta que las propiedades son muy pero muy similares, y es que son opuestas, así como cuando sumas restas, o cuando multiplicas divides, algo así es el caso de la potenciación y radicación, pero bueno, viendo las propiedades tampoco nos da mucha información sino sabemos como aplicarlas a cada caso, para ello vamos a ver los siguientes ejemplos:

Problemas resueltos de la leyes de los Radicales

Para poder entrenarnos ante este tema, y empezar a realizar ejercicios, veamos el siguiente video de Fisimat sobre el tema:

¿Quedó claro el tema?

Entonces empecemos a realizar nuestros ejercicios en la plataforma.

Fisimat,El mejor blog de física y matemáticas.

Iniciamos el mes de octubre con la actitud de seguir publicando artículos sobre los diversos temas de matemáticas, física y química. Por ahora nos toca hablar nuevamente sobre las fracciones parciales pero específicamente sobre el caso de factores lineales repetidos k veces.

Cuando tengamos un factor lineal de la forma mx + b que aparezca repetido k veces en el denominador le corresponderá una suma de fracciones de la siguiente forma

$\displaystyle \frac{{{A}_{1}}}{mx+n}+\frac{{{A}_{2}}}{{{(mx+n)}^{2}}}+\frac{{{A}_{3}}}{{{(mx+n)}^{3}}}+...+\frac{{{A}_{k}}}{{{(mx+n)}^{k}}}$

Dónde $\displaystyle {{A}_{k}}$ es una constante a determinar según sea el caso. Para ello veamos el siguiente ejemplo:

Ejemplos resueltos de Fracciones Parciales con Factor lineal Repetido

Ejemplo 1.- Descomponer en fracciones parciales $\displaystyle \frac{4x+1}{{{(x-1)}^{2}}}$

Si observamos el denominador de la fracción parcial, nos daremos cuenta que el denominador está al cuadrado. O sea que nosotros podríamos expresar la fracción parcial de la siguiente manera:

$\displaystyle \frac{4x+1}{{{(x-1)}^{2}}}=\frac{4x+1}{(x-1)\cdot (x-1)}$

Ahí es donde vemos que asume el nombre de factor lineal repetido, y si se llama lineal es porque lo que se encuentra dentro del paréntesis es un factor lineal, ahí no hay cuadrados y eso es un punto importante porque si fueran cuadrados entonces corresponde a otros casos que veremos más adelante.

Entonces a la fracción parcial le corresponde una suma de fracciones de la siguiente forma:

$\displaystyle \frac{4x+1}{{{(x-1)}^{2}}}=\frac{A}{x-1}+\frac{B}{{{(x-1)}^{2}}}$

El método para encontrar A y B respectivamente es similar al paso del caso 1 de factores lineales no repetidos.

Entonces lo que haremos será multiplicar por el denominador común, es decir el que está elevado al cuadrado y con esto tendríamos lo siguiente:

$\displaystyle 4x+1=(x-1)A+B$

Aplicando propiedad distributiva en el binomio que está con A

$\displaystyle 4x+1=Ax-A+B$

Hasta este punto lo que haremos será lo siguiente, como se trata de una igualdad, si tenemos 4x del lado izquierdo entonces debemos tener 4x de lado derecho; eso quiere decir que A tiene que valor forzosamente 4. Lo mismo pasará para el 1 que tenemos del lado izquierdo, tiene que valor 1 en el lado derecho, por lo que podemos decir que 1 = -A+B

$\displaystyle A=4$

$\displaystyle -A+B=1$

Despejando a B

$\displaystyle B=1+A$

$\displaystyle B=5$

Por lo que B = 5, entonces la descomposición en fracción parcial es:

$\displaystyle \frac{4x+1}{{{(x-1)}^{2}}}=\frac{4}{x-1}+\frac{5}{{{(x-1)}^{2}}}$

Ejercicio Resuelto.

Ejemplo 2.- Descomponer en fracciones parciales la siguiente fracción $\displaystyle \frac{14x+9}{{{(2x+1)}^{2}}}$

Por inspección sabemos que la debemos arreglar de la siguiente forma:

$\displaystyle \frac{14x+9}{{{(2x+1)}^{2}}}=\frac{A}{2x+1}+\frac{B}{{{(2x+1)}^{2}}}$

Multiplicamos nuevamente por el denominador común y nos queda:

$\displaystyle 14x+9=A(2x+1)+B$

Aplicamos propiedad distributiva y nos queda:

$\displaystyle 14x+9=2Ax+A+B$

Recordemos que las “x” deben estar igualadas en ambos miembros, así como los términos que no tienen “x”.

$\displaystyle 14x=2Ax$

$\displaystyle 9=A+B$

En ese pequeño sistema de ecuaciones encontramos los valores de A y B

$\displaystyle A=7$

$\displaystyle B=2$

Por lo que la fracción parcial descompuesta es:

$\displaystyle \frac{14x+9}{{{(2x+1)}^{2}}}=\frac{7}{2x+1}+\frac{2}{{{(2x+1)}^{2}}}$

Y listo problema resuelto.

Aplicación de Fracción Parcial Caso II

Veamos que las fracciones parciales son muy útiles tanto para el cálculo integral como para las famosas transformadas de Laplace. Así que aquí veamos un ejemplo para las integrales.

Esperando que este post haya sido de tu agrado y puedas compartirlo con más amigos o conocidos… Cualquier duda dejarlo en el cajón de comentarios

Fisimat,El mejor blog de física y matemáticas.

Hoy nos toca hablar sobre los sistema de ecuaciones, y es un tema que muchos deberíamos saber. Pues bien muchos fenómenos del mundo real pueden representarse matemáticamente, y algunos de ellos constituyen problemas lineales, es decir, que involucran el manejo de ecuaciones de primer grado, cuya representación gráfica es una línea recta.

Pues bien, en este post vamos a realizar problemas que pueden representarse como un conjunto de ecuaciones con dos incógnitas que de alguna forma u otra constituyen un sistema de ecuaciones; asó como su solución, a través de diversos métodos. Por ejemplo el método gráfico, método de reducción, método de sustitución, de eliminación y en el blog de Laplacianos vamos a observar también la solución a incógnitas por medio de la regla de Cramer y Gauss Jordan.

Sistema de Ecuaciones con Dos Incógnitas

Consideremos el siguiente problema: Se requiere hallar dos números cuya suma sea igual a 10 ¿cuáles son esos números?

Al plantear algebraicamente el problema, se tiene:

x + y = 10

Porque ambos son dos números cualquiera, o sea dos variables. Pero como no tenemos más información al respecto, los valores de de “x” y “y” pueden tomar cualquier valor que cumpla la condición de ser sumados y dar 10.

Por ejemplo:

x = 3, y = 7 –> x + y = 10

x = 7 , y = 3 –> x + y = 10

x = 15, y = -5 –> x+y = 10

x = 0, y = 10 –> x+y = 10

y así podemos seguir hasta encontrar muchísimos valores tanto para “x” como para “y”, y no podríamos ni terminar, por ello se dice que el conjunto solución de este tipo de ecuaciones es infinito.

Una ecuación es una expresión algebraica en forma de igualdad, que posee dos variables o incógnitas y con infinitas soluciones.

Función Lineal

Veamos el siguiente vídeo sobre Función Lineal

Hasta ahora hemos podido asociar valores de las variables para un conjunto solución infinito, pero veamos algo más. ¿Qué pasaría si de una ecuación despejamos a una variable?, Por ejemplo en nuestro caso vamos a despejar a “y” de las siguientes ecuaciones con dos variables, si tienes problemas para despejar, te recomiendo leer este artículo Cómo despejar Fórmulas

x + y = 5

“Despejando”

y = 5 – x

—

3x – 4y = 2

“Despejando”

-4y = 2 – 3x

$\displaystyle y=\frac{2-3x}{-4}=-\frac{1}{2}+\frac{3}{4}x$

Al despejar la variable y la estamos escribiendo en función de x, es decir, a cada valor que asuma x le corresponde uno de y que es su imagen.

Al representar estas funciones en el plano cartesiano, observamos que son rectas, y a estas mismas se les denomina funciones lineales , por lo que podemos decir que:

Una función lineal es una ecuación en la cual las variables están elevadas a la primera potencia. La gráfica de una ecuación lineal con dos variables es una recta en el plano cartesiano

Ejercicios Resueltos con sistemas de dos variables

Bien, es momento de ir por los ejemplos resueltos de un sistema de ecuaciones mediante el método gráfico. Ya que sabemos sobre las funciones lineales que representan rectas, entonces no tendremos problema alguno para comprender los siguientes temas; así que prepárate para responder los problemas.

Ejemplo 1: Del siguiente sistema de ecuaciones encuentre los valores de “x” y de “y”.

$\displaystyle \begin{array}{l}x+y=10\\x-y=5\end{array}$

Solución:

Lo primero que tenemos que hacer es graficar las dos funciones lineales, y si despejamos tendremos algo así:

y = 10 – x (primera ecuación)

-y = 5 – x

y = -5 + x (segunda ecuación)

Al momento de trazar la gráficas correspondientes en cada una de las ecuaciones tendremos algo similar a esto:

Pues nuestra solución si observamos cae prácticamente en x = 7.5 y en el eje “y” cae en y = 2.5

Un sistema de ecuaciones con dos variables expresa dos condiciones en forma de igualdad para las variables. La solución de un sistemas de este tipo está dada por los valores de las variables que, al ser sustituidos en ambas ecuaciones, la satisfacen.

Esto es fácil de asumir, porque lo único que tenemos que hacer es sustituir los valores en las ecuaciones, por ejemplo:

x + y = 10

7.5 + 2.5 = 10 (se cumple).

—

x – y = 5

7.5 – 2.5 = 5 (se cumple).

Ejemplo 2: Del siguiente sistema de ecuaciones encuentre los valores de “x” y “y” , recuerde hacer la comprobación.

$\displaystyle \begin{array}{l}x-y=1\\2x+y=8\end{array}$

Solución:

Para representarlo gráficamente , primero efectuamos una tabulación. Recuerda que bastan dos puntos para determinar una recta. Al momento de realizar la gráfica vamos a encontrar lo que buscamos que es precisamente la solución única.

Despejando las variables, tenemos lo siguiente:

y = x – 1 (primera ecuación)

y = -2x +8 (segunda ecuación)

Ahora trazamos la gráfica

Las soluciones están muy claras, por ejemplo en el eje “x” quedamos en 3, y en el eje “y” quedamos en 2. Por lo tanto nuestro conjunto solución es el par ordenado (3,2).

Un sistema de ecuaciones tiene solución única cuando existe un solo valor para cada variable que satisface ambas ecuaciones. La representación gráfica corresponde a dos rectas que se interceptan en un punto

Ahora hacemos la comprobación.

x – y = 1

sustituyendo

3 -2 = 1 (comprobado).

—

2x + y = 8

2(3) + 2 = 6 +2 = 8 (comprobado).

Fisimat,El mejor blog de física y matemáticas.

El día de hoy platicaremos sobre otro de los métodos del sistema de ecuaciones, para encontrar la solución de un sistema, además del método gráfico, que vimos en el anterior artículo. Existen otros métodos y que iremos viendo en el transcurso del artículo. En este caso nos toca explicar sobre el método de reducción. Éste método consiste que al sumar dos ecuaciones se obtenga otra ecuación, pero con una sola variable, así, al despejar ésta se pueda encontrar el valor de la incógnita. Será un proceso entretenido, ya verás

Es muy importante que para llevar a cabo el proceso de la eliminación de una incógnita de los dos miembros de la ecuación tengamos que multiplicar por números tales que en las dos ecuaciones, los coeficientes de una de las variables sean inversos aditivos.

Pero como siempre decimos, es mucho mejor ver un ejemplo; así que aquí vamos…

Ejercicios Resueltos del Método de Reducción

Ejemplo 1.- Resuelva el siguiente sistema de ecuaciones.

$\displaystyle 2x+y=7$

$\displaystyle x+3y=11$

Solución:

primer paso: Tenemos que elegir la variable que queremos eliminar primero, en este caso vamos a elegir “x” , entonces para poder convertirlo en inverso aditivo, tenemos que multiplicarlo por -2 , a la segunda ecuación, porque haciendo esto al sumar las dos ecuaciones, nos quedaríamos nada más con la que podremos despejar. Así que:

$\displaystyle -2(x+3y)=-2(11)$

$\displaystyle -2x-6y=-22$

segundo paso: Ahora solamente tenemos que sumar la primera ecuación, con la que hemos obtenido de multiplicar por -2.

$\displaystyle \begin{array}{l}2x+y=7\\-2x-6y=-22\end{array}$

Como resultado tenemos.

$\displaystyle -5y=-15$

tercer paso: Procedemos a realizar el despeje de la incógnita.

$\displaystyle y=\frac{-15}{-5}=3$

Por lo que el valor de y es 3.

cuarto paso: Ahora este valor de y = 3 , se sustituye en cualquier ecuación del sistema para obtener el valor de x

$\displaystyle 2x+3=7$

Despejando

$\displaystyle \begin{array}{l}2x=7-3\\x=\frac{4}{2}=2\end{array}$

Por lo que resulta que x = 2 , y = 3

Ejemplo 2: Resuelva el siguiente sistema de ecuaciones:

$\displaystyle \begin{array}{l}3x-2y=-13\\x+4y=5\end{array}$

Solución:

Primer paso: Como bien sabemos, al observar las dos ecuaciones tenemos que elegir una incógnita que deseamos eliminar, para ello hemos seleccionado a la variable y , por lo que para encontrar al inverso aditivo de la segunda ecuación, entonces tenemos que multiplicar por 2 a la primera ecuación.

$\displaystyle \begin{array}{l}2(3x-2y)=2(-13)\\6x-4y=-26\end{array}$

Segundo paso: Ahora si podemos sumar, para poder eliminar la incógnita de “y”.

$\displaystyle \begin{array}{l}6x-4y=-26\\x+4y=5\end{array}$

Quedando así

$\displaystyle \begin{array}{l}7x=-21\\x=-\frac{21}{7}=-3\end{array}$

Tercer paso: Ahora el proceso es sumamente más sencillo, puesto que ya tenemos el valor de una incógnita. Solo falta encontrar la otra. Para ello tomamos la primera ecuación.

$\displaystyle \begin{array}{l}-3+4y=5\\4y=5+3\\y=\frac{8}{4}=4\end{array}$

Ahora podemos decir que ya tenemos todo resuelto.

x = -3 , y = 4

Hasta ahora el proceso de solución debe ser más sencillo, no debe haber problema alguno para encontrar las variables por el método de reducción, que también muchos libros se le conoce como método de suma y resta, pero es exactamente lo mismo.

Ejemplo 3:

Una niña compró en una tienda 2 paletas y un jugo por 7 pesos; al otro día la misma niña compró una paleta y cinco jugos por 17 pesos. ¿Cuánto cuesta cada paleta y cada refresco?

Solución: Sin duda, al tener la habilidad de resolver un sistema de ecuaciones por el método de suma y resta, ya podemos encontrar la solución a problemas de éste tipo, para ello tenemos que fijarnos en los datos que nos dan, y elaborar nuestras ecuaciones.

$\displaystyle \begin{array}{l}2x+y=7\\x+5y=17\end{array}$

Bien en esta ecuación simultánea, procederemos con lo que hemos hecho en los ejemplos 1 y 2.

En este caso nos conviene multiplicar por -2 a la segunda ecuación y sumarlas, para así eliminar la variable “x”

$\displaystyle \begin{array}{l}-2(x+5y)=-2(17)\\-2x-10y=-34\end{array}$

Con esto podemos sumar ambas ecuaciones y observar que nos quedaremos con una sola variable.

$\displaystyle \begin{array}{l}2x+y=7\\-2x-10y=-34\end{array}$

Como resultado tendríamos esto:

$\displaystyle \begin{array}{l}-9y=-27\\y=\frac{-27}{-9}=3\end{array}$

Por lo que tenemos como resultado: y = 3 ; o sea que el precio del jugo es de 3 (pesos, dolares, soles, libras, euros), la moneda por ahora no nos interesa. Solo la cantidad de moneda.

Tomamos una de las ecuaciones iniciales, sustituimos el valor de y = 3 , y con esto tendremos el valor de “x”.

$\displaystyle \begin{array}{l}2x+y=7\\2x=7-y\\x=\frac{7-y}{2}=\frac{7-3}{2}=2\end{array}$

Y de ahí hemos obtenido el valor de x = 2

Entonces podemos concluir de la siguiente forma:

Precio de Paleta = 2 pesos

Precio de Jugo = 3 pesos

Ejemplo resuelto de Método Suma y Resta en Video

Recordemos nuevamente que el método de reducción es el mismo que el método de suma y resta. Así que veamos una explicación a profundidad.

Espero que este tema haya quedado claro, y si tienes dudas por favor dejarlo en la caja de comentarios

Fisimat,El mejor blog de física y matemáticas.

Ey ¡Qué tal!, Hace algunos meses publicábamos en el blog un tema relacionado a las diversas dilataciones, entre ellas mencionamos la dilatación lineal, pero quedaron varias dudas, ya que no se detallaban los demás casos de dilatación como la superficial y la volumétrica. Así que en este post hablaremos de la dilatación superficial.

La dilatación superficial es el incremento proporcional de área o superficie que experimenta cierto objeto con determinada sustancia, de área igual a la unidad, al elevarse su temperatura a un grado centígrado. Este coeficiente muchos autores y libros le han denominado con la letra griega gamma $\displaystyle \gamma$ . El coeficiente de dilatación superficial se usa para los trabajos en sólidos, si se conoce el coeficiente de dilatación lineal de un sólido, entonces su coeficiente de dilatación superficial será dos veces mayor, por lo que tenemos la siguiente relación matemática:

$\displaystyle \gamma =2\alpha$

Por ejemplo, si tenemos el coeficiente de dilatación lineal del cobre que es $\displaystyle 16.7x{{10}^{-6}}$ , por tanto, su coeficiente de dilatación superficial sería:

$\displaystyle \gamma =2\alpha =2(16.7x{{10}^{-6}})=3.34x{{10}^{-5}}{}^\circ {{C}^{-1}}$

Bien, pero para no tener que calcular uno por uno, hemos elaborado una nueva tabla de algunos elementos con su dilatación superficial.

Tabla de Dilatación Superficial

Aquí tenemos la tabla de las sustancias de dilatación superficial que nos servirá para la resolución de ejemplos resueltos.

Al conocer el coeficiente de dilatación superficial de un objeto sólido, prácticamente podemos calcular el área final que tendrá al variar su temperatura conforme a la siguiente fórmula matemática de dilatación superficial.

$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\gamma ({{T}_{f}}-{{T}_{0}}) \right]$

Dónde:

$\displaystyle {{A}_{f}}$ = Área final en unidades en metro cuadrado.

$\displaystyle {{A}_{0}}$ = Área inicial en unidades de metro cuadrado

$\displaystyle \gamma$ = Coeficiente de dilatación superficial

$\displaystyle {{T}_{f}}$ = Temperatura final medida en grados Celcius (°C)

$\displaystyle {{T}_{0}}$ = Temperatura inicial medida en grados Celcius (°C)

Ejercicios Resueltos de Dilatación Superficial

Bien, ningún problema en Física se puede entender sino se hace uso de los ejercicios. Así que llegó el momento de practicar.

Problema 1.- En una escuela preparatoria una venta de vidrio tiene un área de 1.4 m^2 , si la temperatura está a 21°C. ¿Cuál será su área final al aumentar la temperatura a 35°C?

Solución: Bien, como siempre debemos considerar los datos que tenemos, y los implícitos, aquellos que no están en el problema pero que nos proporcionan pistas.

Sabemos que se trata de la sustancia del vidrio, por lo que debemos considerar su coeficiente de dilatación superficial, a su vez tenemos un área inicial de 1.4 metros cuadrados, y una variación de la temperatura inicial de 21°C hasta 35°C. Entonces la incógnita es el área final, variable que afortunadamente ya la tenemos despejada.

Si tienes problemas con el despeje, te recomendamos ver el artículo de como despejar fórmulas

$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\gamma ({{T}_{f}}-{{T}_{0}}) \right]$

Sustituimos nuestros datos en la fórmula

$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left[ 1+14.6x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 35{}^\circ C-21{}^\circ C \right) \right]$

Luego

$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left[ 1+204.4x{{10}^{-6}} \right]$

Ahora realizamos la suma del paréntesis.

$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\cdot 1.0002044$

Lo que nos da como resultado

$\displaystyle {{A}_{f}}=1.40028616{{m}^{2}}$

Problema 2.- A una temperatura de 40°C una puerta de aluminio mide 2.4 m de largo y 0.9 de ancho. ¿Cuál será su área final al disminuir su temperatura a 23°C?

Solución: Nuevamente en el problema nos piden el área final, por lo tanto seguiremos usando la misma fórmula que el ejercicio anterior, solamente debemos tener cuidado con nuestros datos, ya que sabemos que se trata de una puerta de aluminio, con ello ya tenemos el dato del coeficiente de dilatación superficial, nos hace falta área inicial, solamente. ¿Cómo la obtenemos?.

Pues fácilmente, sabemos que se trata de una puerta, así que calculemos el área por sus dimensiones a lo largo y ancho. Así que sería:

$\displaystyle {{A}_{0}}=(2.4m)(0.9m)=2.16{{m}^{2}}$

Una vez teniendo este dato, procedemos a sustituir en la fórmula. Pero claro, teniendo en cuenta el valor de el coeficiente de dilatación superficial.

$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\gamma ({{T}_{f}}-{{T}_{0}}) \right]$

Ahora tenemos.

$\displaystyle {{A}_{f}}=2.16{{m}^{2}}\left[ 1+44.8x{{10}^{-6}}(23{}^\circ C-40{}^\circ C) \right]$

$\displaystyle {{A}_{f}}=2.16{{m}^{2}}\cdot 0.9992384$

Multiplicando tenemos.

$\displaystyle {{A}_{f}}=2.15835494{{m}^{2}}$

Qué sería nuestro resultado.

Fisimat,El mejor blog de física y matemáticas.

Ya hemos hablado sobre la dilatación lineal, la dilatación superficial y ahora terminamos estos tres capítulos hablando de la dilatación cúbica o dilatación volumétrica que significan lo mismo. Para ello debemos de tener en cuenta que el proceso de dilatación cúbica hace referencia al aumento de las dimensiones de un objeto a lo largo, ancho y alto, o sea que en términos geométricos tenemos un incremento de volumen. En este estudio hay que considerar el coeficiente de dilatación cúbica que nos hace hincapié al incremento relativo de volumen que experimenta un objeto de determinada sustancia, preferente de un volumen igual a la unidad, al elevar su temperatura un grado Celsius.

Este coeficiente se determina mediante la letra griega beta $\displaystyle \beta$ .Por lo general este coeficiente de dilatación se usa para los líquidos, matemáticamente tenemos la relación de que la dilatación volumétrica es tres veces mayor que la dilatación lineal.

$\displaystyle \beta =3\alpha$

Podemos hacer una comprobación muy sencilla , por ejemplo; si sabemos que el coeficiente de dilatación lineal del acero es $\displaystyle 11.5x{{10}^{-6}}{}^\circ {{C}^{-1}}$ , entonces el coeficiente de dilatación volumétrica sería:

$\displaystyle \beta =3\alpha =3(11.5x{{10}^{-6}}{}^\circ {{C}^{-1}})=34.5x{{10}^{-6}}{}^\circ {{C}^{-1}}$

¿Se entendió?

Entonces dejamos la tabla para no tener problemas al resolver los ejercicios propuestos.

Tabla de Dilatación Cúbica

Colocamos la siguiente tabla, y debemos considerarlo.

Como bien sabemos, al conocer la dilatación cúbica de cualquier sustancia, entonces podemos calcular el volumen final que tendrá la sustancia, mediante la siguiente fórmula.

$\displaystyle {{V}_{f}}={{V}_{0}}\left[ 1+\beta \left( {{T}_{f}}-{{T}_{0}} \right) \right]$

Dónde:

$\displaystyle {{V}_{f}}$ = Volumen Final en Metro Cúbico

$\displaystyle {{V}_{0}}$ = Volumen Inicial en Metro Cúbico

$\displaystyle \beta$ = Coeficiente de Dilatación Cúbica

$\displaystyle {{T}_{f}}$ = Temperatura Final en Grados Celcius

$\displaystyle {{T}_{0}}$ = Temperatura Inicial en Grados Celcius

Antes de resolver algunos ejemplos resueltos, necesitamos forzosamente tener en cuenta las siguientes anotaciones.

1.- En el caso de los sólidos que no están uniformes, es decir; aquellos sólidos que poseen algún hueco en su textura, debe considerarse como si estuviera lleno del mismo material, es decir, como si fuera totalmente sólido.

2.- Para la dilatación cúbica en los líquidos hay que tomar en cuenta que cuando se ponen a calentar, también se calienta el recipiente que los posee, el cual al dilatarse aumenta también su capacidad calorífica. Por ello, el aumento real del volumen del líquido será igual al incremento de volumen del objeto que los contiene o sea el recipiente más el aumento del volumen del líquido en el recipiente graduado.

3.- El coeficiente de dilatación volumétrica es igual para todos los gases, ¿ por qué? porque, al ser sometido a una presión constante, por cada grado Celsius que cambie su temperatura variará 1/273 el volumen que ocupaba a 0° celcius.

Ejercicios Resueltos de Dilatación Volumétrica

Problema 1.- Una barra de aluminio de 0.5 metros cúbicos de volumen, experimenta inicialmente una temperatura de 14°C, posteriormente se calienta a 45°C , ¿cuál será su volumen final? ¿qué tanto ha incrementado?

Bosquejo del Problema 1

Solución:

Como siempre, tenemos que recoger nuestros datos iniciales para poder aplicar la fórmula, por lo que primero debemos pensar en el material que está sufriendo el cambio de temperatura, que es el aluminio. Por lo que esto sería:

$\displaystyle \beta =67.2x{{10}^{-6}}{}^\circ {{C}^{-1}}$

$\displaystyle {{V}_{0}}=0.5{{m}^{3}}$

$\displaystyle {{T}_{0}}=14{}^\circ C$

$\displaystyle {{T}_{f}}=45{}^\circ C$

Aplicando la fórmula:

$\displaystyle {{V}_{f}}=0.5{{m}^{3}}\left[ 1+67x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 45{}^\circ -14{}^\circ \right) \right]$

$\displaystyle {{V}_{f}}=0.5{{m}^{3}}\left[ 1+67x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 31{}^\circ \right) \right]$

Luego

$\displaystyle {{V}_{f}}=0.5{{m}^{3}}\left[ 1+2.077x{{10}^{-3}} \right]$

Sumando

$\displaystyle {{V}_{f}}=0.5{{m}^{3}}\left[ 1.002077 \right]$

Y finalmente tenemos el volumen final

$\displaystyle {{V}_{f}}=0.5010385$

Si queremos saber que tanto se incrementó, entonces basta con hacer una simple resta entre el volumen final y el volumen inicial, quedando la operación:

$\displaystyle \Delta V=0.5010385-0.5$

$\displaystyle \Delta V=0.0010385$

Fisimat,El mejor blog de física y matemáticas.

¿Qué tal? Hoy tenemos un tema muy entretenido en Física, especialmente del área de la hidráulica, y es que se trata de la densidad y peso especifico, uno de los temas que nos aporta muchísimo valor en el campo de los fluidos.

No olvidemos que dentro del tema de la hidráulica hay muchos conceptos que debemos de tener en cuenta antes de abordar cualquier tema relacionado a este campo, por ejemplo las siguientes definiciones que conforman a la Hidráulica en sí. Los líquidos poseen características tales como la viscosidad, tensión superficial, cohesión, adherencia y capilaridad. Y cada una de ellas
se originan y presentan de diversas formas. Por ejemplo:

La viscosidad se da por el rozamiento de unas partículas con otras, cuando el líquido fluye; la tensión superficial se presenta debido a la atracción entre algunas moléculas del líquido por lo que la superficie libre de cualquier líquido se comporta como una finísima membrana elástica, ahora con la cohesión; la cohesión no es más que la fuerza que mantiene unidas a las moléculas de una misma sustancia, a diferencia de la adherencia que es la fuerza de atracción que se manifiesta en moléculas de dos sustancias diferentes, y finalmente tenemos a la capilaridad que se presenta cuando existe contacto entre un líquido y una pared sólida, especialmente si son tubos muy delgados, llamados capilares.

La densidad de una sustancia, también llamada por algunos autores como la “masa específica“, es una propiedad de la materia que expresa a la masa contenida por unidad de volumen. Su fórmula es:

$\displaystyle \rho =\frac{m}{V}$

Donde la letra RO Griega simboliza a la densidad, Sus unidades en el SI (Sistema Internacional), son en kg/m^3 (kilogramo sobre metro cúbico).

Por otro lado:

El peso específico de una sustancia es también una propiedad característica; su valor está determinando por el cociente entre el peso por unidad de volumen, matemáticamente esto es:

$\displaystyle {{P}_{e}}=\frac{P}{V}$

Dónde:

Pe = Peso específico (N/m^3) “Newton sobre metro cúbico”

P = Peso de la sustancia en Newtons (N).

V = Volumen que ocupa la sustancia en metro cúbicos (m^3).

Bien, ahora veamos algunos ajustes matemáticos que podemos realizar para obtener fórmulas nuevas a través de las que ya tenemos. Por ejemplo, recordemos que el peso es igual a la masa por gravedad, o sea.

$\displaystyle P=mg$

Como sabemos que el peso específico es Peso sobre Volumen, sustituyamos el Peso de masa por gravedad en la fórmula de peso específico.

$\displaystyle {{P}_{e}}=\frac{P}{V}=\frac{mg}{V}$

Pero recordemos que la densidad es igual a masa sobre volumen, entonces podemos simplificar la fórmula:

$\displaystyle {{P}_{e}}=\frac{P}{V}=\frac{mg}{V}=\rho g$

Por lo que ya tenemos nueva fórmula para calcular el peso especifico.

Tabla de valores de Densidad y Peso Específico

Aquí se ilustran algunos valores de densidad y peso específico que nos serán de gran utilidad para la resolución de problemas.

Sustancia	Densidad (Kg/m³)	Peso Específico (N/m³)
Agua (4° C)	1000	9,800
Alcohol	790	7,742
Aceite	915	8,967
Hielo	920	9,016
Madera	430	4,214
Oro	19,320	189,336
Hierro	7,860	77,028
Mercurio	13,600	13,280
Oxigeno (0°)	1.43	14.014
Hidrógeno (0°)	0.09	0.882

Ejercicios Resueltos de Densidad y Peso Especifico

Bien, ahora es momento de practicar, de poner en práctica parte de la teoría aquí aprendida.

Tomar en cuenta algunos factores de conversión que podamos usar dentro de los ejercicios aquí propuestos:

1000 gramos = 1 Kilogramo

1000000 centímetros cúbicos = 1 metro cúbico

Problema 1.- Un cuerpo sólido de cierto material, se midió su masa y se encontró un valor de 700 gramos; al medir su volumen éste fue de 2,587 centímetros cúbicos. Calcular la densidad en el SI (Sistema Internacional).

Solución: En este ejemplo, tenemos el dato de la masa de 700 gramos de hierro, y a su vez un volumen de 2587 centímetros cúbicos, entonces nuestros datos no están en el sistema internacional, por lo que haremos una sencilla conversión.

Datos:

$\displaystyle m=700g\left( \frac{1kg}{1000g} \right)=0.7kg$

$\displaystyle V=2587c{{m}^{3}}\left( \frac{1{{m}^{3}}}{1000000c{{m}^{3}}} \right)=2.587x{{10}^{-3}}{{m}^{3}}$

Aplicando la fórmula.

$\displaystyle \rho =\frac{0.7kg}{2.587x{{10}^{-3}}{{m}^{3}}}=270.58\frac{kg}{{{m}^{3}}}$

Qué sería la densidad de dicho material.

Problema 2.- 0.5 kg de alcohol etílico ocupan un volumen de 0.000544 metros cúbicos. Calcular:

a) ¿La densidad del alcohol etílico?

b) ¿Cuál es su peso específico?

Solución: Este problema nos aporta la mayor cantidad de datos que necesitamos para poder calcular.

$\displaystyle \rho =\frac{0.5kg}{0.000544{{m}^{3}}}=919.118\frac{kg}{{{m}^{3}}}$

Ahora veamos el peso específico

$\displaystyle {{P}_{e}}=\left( 919.118\frac{kg}{{{m}^{3}}} \right)(9.8\frac{m}{{{s}^{2}}})=9007.35\frac{N}{{{m}^{3}}}$

Problema 3.- Calcular la masa y el peso de 14500 litros de gasolina. Si la densidad de la gasolina es de 700 kg/m^3.

Solución: Este problema nos advierte sobre el peso de la gasolina, y su densidad, por lo que solo tendremos que buscar la fórmula correspondiente y resolver.

Por la fórmula de densidad, podemos hacer el despeje de la variable masa, quedando así:

$\displaystyle m=\rho V$

Sin embargo, no podemos colocar el volumen todavía porque tendríamos que hacer nuestra conversión de litros a metros cúbicos. Para ello:

$\displaystyle 14500l\left( \frac{1{{m}^{3}}}{1000l} \right)=14.5{{m}^{3}}$

Ahora si podemos aplicar la fórmula de la masa:

$\displaystyle m=\left( 700\frac{kg}{{{m}^{3}}} \right)\left( 14.5{{m}^{3}} \right)=10150kg$

y para calcular el peso. Solamente multiplicamos por la gravedad.

$\displaystyle P=(10150kg)(9.8\frac{m}{{{s}^{2}}})=99470N$

Problema 4.- ¿Cuál es la densidad de un aceite cuyo peso específico es de 6578 N/m^3?

Solución: Es momento de anotar nuestros datos y observar que fórmula usaremos.

Sabemos que el peso específico la podemos expresar en función de la densidad de la siguiente forma:

$\displaystyle \rho =\frac{{{P}_{e}}}{g}=\frac{6578\frac{N}{{{m}^{3}}}}{9.8\frac{m}{{{s}^{2}}}}=671.22\frac{kg}{{{m}^{3}}}$

Con lo que damos con la densidad de dicho aceite.

Problemas Reto-Placianos

Colocaremos algunos problemas para que los resuelvas con calma en tu libreta, dejar en los comentarios tus resultados.

Problema 5.- Calcular el peso específico del oro cuya densidad es de 19300 kg/m^3

Problema 6.- ¿Qué volumen debe tener un tanque para que pueda almacenar 3040 kg de gasolina cuya densidad es de 680 kg/m^3?

Problema 7.- Calcular la densidad de un prisma rectangular cuyas dimensiones son: largo 6cm, ancho 5 cm, alto 3 cm, y tiene una masa de 300 g; calcular el volumen que ocupará un objeto de la misma sustancia si tiene una masa de 100 g.

Fisimat,El mejor blog de física y matemáticas.

Sin duda, el principio de Arquímedes es una gran herramienta en la física, principalmente en el área de la hidráulica, nos aporta un gran valor y conocimiento para entender por ejemplo la flotación de los cuerpos, otros conceptos y quizá hasta encontrar la respuesta que derivan de éste descubrimiento como el, ¿por qué flotan los barcos en el mar?, entonces, haciendo mención a ello, vamos a explicar la teoría y después como es costumbre pasaremos a ver problemas resueltos sobre éste principio.

Si te has dado cuenta, cuando un cuerpo es sumergido en un líquido, éste cuerpo ejerce una empresión vertical ascendente (como si empujara para no ser sumergido), puedes experimentarlo con una pelota en un estanque, o en la alberca. Pues bien el empuje que reciben los cuerpos al ser introducidos en un líquido fue la investigación que nos aportó el gran genio de la antigua Grecia el gran Arquímedes, además de ser un hombre destacado también exploró en otros fenómenos tales como las palancas, la geometría plana y del espacio, y su teoría sobre los números.

El principio de Arquímedes estipula lo siguiente:

Todo cuerpo que está sumergido en un fluido, recibe un empuje ascendente igual al peso del fluido desalojado

Para el principio de Arquímedes tenemos varios casos, de acuerdo a la magnitud de dos fuerzas que son el peso que lo empuja hacía abajo, y el empuje del líquido que lo impulsa hacia arriba. Hablando de un cuerpo sumergido.

Casos del Principio de Arquimedes

1.- Si la magnitud del peso del cuerpo es menor a la magnitud de empuje.

Caso 1

Para el primer caso, podemos tener que la magnitud del peso del cuerpo sea menor a la magnitud del empuje que recibe, flota porque desaloja la menor cantidad del líquido que su volumen.

2.- Si la magnitud del peso es igual a la magnitud de empuje

Caso 2

Como segundo caso tenemos, que la magnitud del peso del cuerpo sea igual a la magnitud del empuje que recibe, esto hará que el cuerpo permanezca en equilibrio, o lo que hace alusión a tener el cuerpo sumergido dentro del líquido.

3.- Si la magnitud del peso del cuerpo es mayor que la magnitud del empuje

Caso 2

Aquí es el caso cuando experimentamos que el cuerpo se hunde. O sea como el enunciado lo menciona, la magnitud del peso del cuerpo es mayor a la magnitud del empuje, y lógicamente al estar completamente sumergido el cuerpo desalojará un volumen del líquido igual a su volumen.

Podemos con esto respondernos que para que un barco flote debe desalojar un volumen de líquido cuyo peso sea igual al del barco.

Ejercicios Resueltos del Principio de Arquímedes

Bien ahora que sabemos muy bien el tema de la densidad de algunos cuerpos, y conocemos la teoría básica del principio de flotabilidad, podemos decir que:

Para que un cuerpo flote en cualquier fluido, su densidad promedio debe ser menor a la del fluido.

La magnitud del empuje que recibe un cuerpo sumergido en un determinado líquido se calcula multiplicado el peso específico del líquido por el volumen desalojado

Esto tiene por fórmula:

$\displaystyle E={{P}_{e}}V$

Ahora si pasemos a los ejemplos resueltos.

Problema 1.- Un cubo de hierro de 20 cm de arista se sumerge totalmente en agua. Si tiene un peso con una magnitud de 560.40 N, calcular:

a) ¿Qué magnitud de empuje recibe?

b) ¿Cuál será la magnitud del peso aparente del cubo?

Solución: Lo primero que haremos será considerar los datos y empezar a sustituir en las fórmulas que tengamos a disposición.

Recordemos que para calcular el empuje, es necesario tener el volumen y el peso específico. Para calcular el volumen basta primero en convertir las unidades de la arista a metros (SI) unidades del Sistema Internacional.

Datos:

$\displaystyle l=20cm\left( \frac{1m}{100cm} \right)=0.2m$

$\displaystyle P=560.4N$

$\displaystyle V=(0.2m)(0.2m)(0.2m)=8x{{10}^{-3}}{{m}^{3}}$

El peso específico del agua es:

$\displaystyle {{P}_{e}}\left( {{H}_{2}}O \right)=9800\frac{N}{{{m}^{3}}}$

Ahora si podemos comenzar a resolver.

a) Calculando el Empuje

$\displaystyle E={{P}_{e}}V=(9800\frac{N}{{{m}^{3}}})(8x{{10}^{-3}}{{m}^{3}})=78.4N$

b) Calculando el Peso aparente

$\displaystyle {{P}_{aparente}}={{P}_{real}}-Empuje$

$\displaystyle {{P}_{aparente}}=560.4N-78.4N=482N$

Fisimat,El mejor blog de física y matemáticas.

El día de hoy hablaremos sobre el gasto y flujo un tema muy útil en la hidrodinámica aquella área de la física que estudia la hidráulica y que se encarga de estudiar a los fenómenos de los líquidos en movimiento, y pone en evidencia aportes grandes como el diseño de canales, puertos, presas, hélices, turbinas, etc. Así que para entender éste tema solamente necesitas leer bien, entender la teoría y resolver ejercicios

Hay que considerar algunos puntos importantes en el estudio de la hidrodinámica, antes de continuar:

1.- Los líquidos en su totalidad son incomprensibles

2.- Debemos considerar despreciable a la viscosidad, recordando qué estos principios son ideales, por lo que evitaremos la resistencia al flujo, así como omitir las pérdidas de energía mecánica producidas por la viscosidad.

3.- El flujo debe suponerse estacionario o estable. Ya que esto ocurre cuando la magnitud de la velocidad de toda partícula del líquido es similar al pasar por el mismo punto.

¿A qué le llamamos Gasto?

Bien, el gasto es un concepto en física que advierte que cuando un líquido fluye a través de cierta tubería hay una relación entre el volumen del líquido y el tiempo que éste tarda en fluir.

Para ello veamos su fórmula:

$\displaystyle G=\frac{V}{t}$

Dónde:

G = gasto en $\displaystyle \frac{{{m}^{3}}}{s}$

V = volumen del líquido que fluye en metros cúbicos $\displaystyle {{m}^{3}}$

t = tiempo que tarda en fluir el líquido en segundos (s)

Bien, pero no es la única fórmula para poder obtener el gasto, existe otra fórmula que relaciona la magnitud de la velocidad del líquido y el área de la sección transversal de la tubería.

Para conocer por ejemplo el volumen de líquido que pasa de la primera sección de área a la segunda sección, basta con multiplicar el área, la magnitud de la velocidad del líquido y el tiempo que tarda en pasar por los puntos. Muy fácil ¿no?

$\displaystyle V=Avt$

De ésta misma fórmula podemos obtener la segunda fórmula de la que hemos hablado.

$\displaystyle G=\frac{Avt}{t}=Av$

Dónde

G = gasto en $\displaystyle \frac{{{m}^{3}}}{s}$

A = área de la sección transversal de la tubería, medida en metros cuadrados.

v = magnitud de la velocidad del líquido en m/s

¿Qué es el flujo?

Bien, así como vimos el concepto del gasto, el flujo no es más que la cantidad de masa del líquido que fluye a través de una tubería en unidad de tiempo.

Dada por la siguiente fórmula:

$\displaystyle F=\frac{m}{t}$

Dónde:

F = flujo en kg/s

m = masa del líquido en unidades de kg (kilogramos)

t = tiempo que tarda en fluir en segundos (s)

Bien, pero así como el gasto, existe otra fórmula derivada de la densidad que nos permite obtener el flujo.

Como sabemos, la densidad de un cuerpo es la relación entra la masa y volumen, entonces obtenemos:

$\displaystyle \rho =\frac{m}{V}$

Despejando a la “masa”

$\displaystyle m=\rho V$

Entonces de la ecuación que tenemos de flujo, reemplazamos a la “masa” por la nueva forma de la densidad.

$\displaystyle F=\frac{\rho V}{t}$

Pero la podemos dejar en términos del Gasto, ya que el gasto es:

$\displaystyle G=\frac{V}{t}$

Entonces:

$\displaystyle F=G\rho$

Dónde el Gasto por la densidad nos da el flujo.

Ejercicios Resueltos de Gasto y Flujo

Para empezar a entender los siguientes ejemplos de gasto y flujo, es importante repasar los ejercicios por tu cuenta, y así evitar problemas de comprensión.

Problema 1.- Calcular el gasto de agua que pasa a través de una tubería al fluir $\displaystyle 1.8{{m}^{3}}$ en medio minuto.

Solución: Lo primero que haremos será analizar nuestros datos:

G = ?

V = $\displaystyle 1.8{{m}^{3}}$

t = $\displaystyle 0.5\min \left( \frac{60s}{1\min } \right)=30s$

Aplicando la fórmula de Gasto:

$\displaystyle G=\frac{1.8{{m}^{3}}}{30s}=0.06\frac{{{m}^{3}}}{s}$

Problema 2.- Calcular el tiempo que tardará en llenarse un tanque cuya capacidad es de 8 m^3 al suministrarle un gasto de 60 l/s

Solución: Coloquemos nuestros datos:

t = ?

V = 8 m^3

G = 60 l/s

No podemos manejar el gasto con unidades de (litro/segundo) , por lo que debemos de convertir esos litros a metros cúbicos, el factor de conversión es 1 metro cúbico = 1000 litros.

$\displaystyle G=60\frac{l}{s}\left( \frac{1{{m}^{3}}}{1000l} \right)=0.06\frac{{{m}^{3}}}{s}$

Una vez teniendo el Gasto en las unidades del SI (Sistema Internacional), ahora es momento de ver la fórmula a utilizar:

$\displaystyle G=\frac{V}{t}$

Despejando al tiempo “t”

$\displaystyle t=\frac{V}{G}$

Sustituyendo

$\displaystyle t=\frac{V}{G}=\frac{8{{m}^{3}}}{0.06\frac{{{m}^{3}}}{s}}=133.33s$

Algo aproximado a los 2 minutos con 22 segundos

Problema 3.- Determinar el diámetro que debe tener una tubería, para que el gasto sea de 0.5 m^3/s a una velocidad de 6 m/s .

Solución: Bien, este problema requiere de un análisis más minucioso a los ejercicios anteriores, pero partamos de nuestros datos:

d = ?

G = 0.5 m^3/s

v = 6 m/s

Hay una fórmula del gasto que menciona la relación entre la velocidad y el área, por lo que usaremos esa:

$\displaystyle G=vA$

Vamos a despejar al “área” ya que de ahí podremos calcular el diámetro circular de la tubería.

$\displaystyle A=\frac{G}{v}$

Sustituyendo datos en la fórmula:

$\displaystyle A=\frac{G}{v}=\frac{0.5\frac{{{m}^{3}}}{s}}{6\frac{m}{s}}=0.0833{{m}^{2}}$

Pero si nos referimos al área de un círculo, sabemos que:

$\displaystyle A=\frac{\pi {{d}^{2}}}{4}$

Despejando al “diámetro”

$\displaystyle d=\sqrt{\frac{4A}{\pi }}$

Ahora es momento de obtener el diámetro en la fórmula:

$\displaystyle d=\sqrt{\frac{4\left( 0.0833 \right)}{\pi }}=0.326m$

Lo que nos da un diámetro de 0.326 metros.

Problema 4.- Por una tubería fluyen 2300 litros de agua en un minuto, calcular:

Dato: densidad del agua 1000 kg/m^3

a) El gasto

b) El flujo

Solución: Bien, lo primero es tomar los datos que nos aporta el problema, así que:

G = ?

F = ?

V = 2300 litros

t = 1 minuto = 60 segundos

Necesitamos convertir los 2300 litros a metros cúbicos, para ello recurrimos a nuestro factor de conversión.

$\displaystyle V=2300l\left( \frac{1{{m}^{3}}}{1000l} \right)=2.3{{m}^{3}}$

Ahora si podemos calcular el gasto:

$\displaystyle G=\frac{2.3{{m}^{3}}}{60s}=0.0383\frac{{{m}^{3}}}{s}$

Teniendo el gasto, pasemos a calcular el flujo, que es el producto del gasto por la densidad del líquido.

$\displaystyle F=G\rho =(0.0383\frac{{{m}^{3}}}{s})(1000\frac{kg}{{{m}^{3}}})=38.3\frac{kg}{s}$

Lo que equivale a tener 38.3 kilogramos de agua por cada segundo.

Fisimat,El mejor blog de física y matemáticas.